очевидно при n = 1 не существует графа с 2 ребрами, поэтому n ≥ 2
степень вершины - количество всех ребер, выходящих из вершины deg(v)
сумма степеней всех вершин равна удвоенному количеству всех ребер
т.е. в данном графе сумма степеней вершин
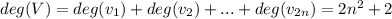
будем доказывать от противного. предположим такого ребра нет.
рассмотрим любые 4 вершины, чтобы среди них не было ребра, которое принадлежит двум циклам длины 3, среди них может быть проведено не более 4 ребер, как бы не проводили пятое, всегда оно дополнит второй цикл.
поэтому сумма степеней всех вершин среди любых четырех не превосходит 4*2 = 8
рассмотрим четверки:
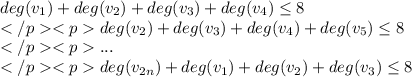
сложим все неравенства и получим, что
4*deg(V) ≤ 16n
deg(V) ≤ 4n
но deg(V) по условию равно 2n² + 2
2n² + 2 ≤ 4n
2(n-1)² ≤ 0
неравенство может выполниться только при n = 1, но как уже было отмечено, этот случай не удовлетворяет по условию.
Значит, наше предположение было не верно.
ответ: доказано.
Пошаговое объяснение:
на 5 остатки все, что меньше числа 5 : 1, 2, 3, 4
на 8 остатки все, что меньше 8: 1, 2, 3, 4, 5, 6, 7
на 10 остатки все, что меньше 10: 1, 2, 3, 4, 5, 6, 7, 8, 9
например 11:5=2 ост.1, 12:5=2 ост.2, 13:5=2 ост.3, 14:5=2 ост.4, 15:5 =3 уже без остатка. Деление без остатка на 5 числа которые заканчиваются на 0 и 5 ( 5, 10, 15, 20, 25 и т.д.)
9:8=1 ост.1, 10:8=1 ост.2 и т.д. 15:8=1 ост.7, а вот 16:8=2 без остатка. 8, 16, 24, 32, 48 и т.д. деление на 8 без остатка.
11:10=1 ост.1, 12:10=1 ост.2, и т.д. все числа которые заканчиваются на нуль 0.