Пошаговое объяснение:
2х-у+4=0
если решать как хотите вы,то тогда получается так
2х- (у-4)=0 , где (у-4) будет вычитаемое
у-4=2х-0 получаем
у-4=2х если У уменьшаемое,то по правилу нахождения уменьшаемого,надо к разности прибавить вычитаемое
у= 2х+4
и при х=4 получим у=2*4+4 у=8+4 у=12
или применяя правила переноса
2х-у+4=0
2х+4=у
при х=4 получаем 2*4+4=у 12=у
поздно увидела ваш комментарий,что вычитаемое просто У
тогда будем делать так.
2х-у+4=0
(2х+4) -у=0 здесь уменьшаемое вся скобка (2х+4)
у=2х+4 -0
при х=4 у=2*4+4 у=8+4 у=12
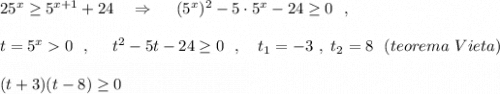
Решаем неравенство методом интервалов .
Нули функции t= -3 и t=8 . Отметим эти числа на оси . Подсчитаем знаки в образовавшихся интервалах . И выберем те интервалы, где записан знак плюс . Учтём, что неравенство нестрогое, значит граничные точки будут включаться в решение .
![+++[-3\, ]---[\ 8\ ]+++\ \ \ \ \ \ t\in (-\infty ;-3\ ]\cup [\ 8\ ;+\infty \, )](/tpl/images/4978/0732/2171e.png)
Учитывая, что t > 0 , выбираем только второй промежуток .
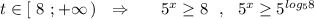
Так как показательная функция с основанием, большим 1 , возрастающая, то знак между аргументами функций будет таким же, как и знак между самими функциями .
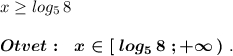Наименьшее из предложенных чисел из указанного промежутка равно 
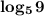, так как 
,
.
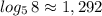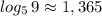Можно сравнить так: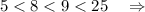 
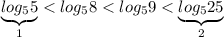
V=1200х5х4=2400см в кубе