Пошаговое объяснение:
Первый столбик:
7/9 * 3/7 = 1/3
7/9 : 3/7 = 7/9 * 7/3 = 49/27 = 1 22/27
Второй столбик:
1 3/5 : 2 1 /2 = 8/5 * 2/5 = 16/25 - это b
1 3/5 * 16/25 = 8/5 * 16/25 = 128/ 125 = 1 3/125
Третий столбик
1 : 5/14 = 1*14/5 = 14/5 = 2 4/5 - это а
14/5 : 5/14 = 14/5 * 14/5 = 196/25 = 7 21/25
Четвертый столбик:
10 : 5 = 2 - это b
5 : 2 = 5/2 = 2 1/2
Пятый столбик:
1 24/25 * 1 2/3 = 49/25 * 5/3 = 49/15 = 3 4/15
1 24/25 : 1 2/3 = 49/25 *3/5 = 147/125 = 1 22/125
Шестой столбик:
1 : 8 1/3 = 1* 3/25 = 3/25 - это b
8 1/3 : 3/25 = 25/3 * 25/3 = 625/9 = 69 4/9
Седьмой столбик:
3 1/3 : 7/10 = 10/3 * 10/7 = 100/21 = 4 16/21 - это b
7/10 : 100/21 = 7/10 *21/100 = 147/1000
Восьмой столбик:
8* 5 1/3 = 8/1 * 16/3 = 128/3 = 42 2/3 - это а
42 2/3 * 5 1/3 = 128/3 * 16/3 = 2048/9 = 227 5/9
Рассмотрим первое слагаемое (82n). Произведение четного числа на любое другое целое дает нам четное число (правило 2).
Второе слагаемое должно быть нечетным, так как произведение двух нечетных чисел нечетно (правило 1).
И сумма четного и нечетного чисел обязательно нечетна (3), искомое число будет нечетным, что и требовалось доказать!
Примечание:
Необходимые правила:
(1) Если нечетное число умножить на нечетное, то получится тоже нечетное (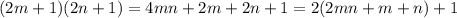 ).(2) Произведение четного числа на любое натуральное (или целое) всегда будет четным (если умножаем на нечетное:
).(2) Произведение четного числа на любое натуральное (или целое) всегда будет четным (если умножаем на нечетное: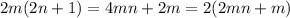 ; если на четное:
; если на четное: 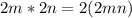 ).(3) Если сложить четное и нечетное числа, то получится нечетное число (
).(3) Если сложить четное и нечетное числа, то получится нечетное число (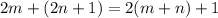 ).
).
24ц=2400000гр