В решении.
Пошаговое объяснение:
Какие из следующих величин являются прямо пропорциональными, обратно пропорциональными и какие ни теми., ни другими?
Зависимость прямо пропорциональная - когда с увеличением одной величины увеличивается другая.
Зависимость обратно пропорциональная - когда с увеличением одной величины другая уменьшается.
1)Количество товара и его стоимость - чем больше товара, тем больше он стоит, прямо пропорциональная зависимость.
2)Скорость движения и время, необходимое для преодоления данного пути - чем выше скорость, тем меньше времени в пути, обратно пропорциональная зависимость.
3)Масса воды и ее объем - чем больше объём воды, тем больше её масса, прямо пропорциональная зависимость.
4)Скорость движения и длина пути, пройденного за определенное время - чем выше скорость, тем больше длина пути, прямо пропорциональная зависимость.
5)Длина и ширина прямоугольника данной площади. - нет зависимости.
6)Сторона квадрата и его площадь - чем больше сторона квадрата, тем больше его площадь, прямо пропорциональная зависимость.
7)Рост человека и его возраст - нет зависимости, когда человек вырос, а пока растёт - прямо пропорциональная, чем старше, тем выше.
Пусть катет треугольника равен а. Тогда гипотенуза равна 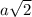 .
.
Есть два составлять квадрат.
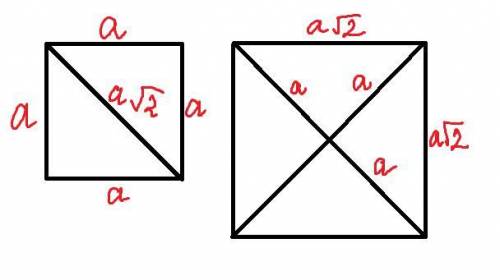
1. Составим из двух таких треугольников квадратик (треугольники совместим по гипотенузе). Так как треугольников дано 50, то квадратиков мы можем получить вдвое меньше, то есть 25. Уже из таких квадратиков (сторона которых равна а) будем составлять разные квадраты.
Первый квадрат - это один такой квадратик (сторона а)
Далее, квадрат из 4 квадратиков (сторона 2а)
Квадрат из 9 квадратиков (сторона 3а)
Квадрат из 16 квадратиков (сторона 4а)
Квадрат из 25 квадратиков (сторона 5а)
Больше 25 квадратиков мы использовать не можем.
Итого, у нас получилось 5 различных квадратов.
2. Составим из четырех таких треугольников квадратик (треугольники совместим по катетам). Так как треугольников дано 50, то таких квадратиков можем получить в четыре раза меньше, то есть 12 (еще два треугольника останутся незадействованными). Из таких квадратиков (сторона которых равна 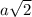 как гипотенуза исходного треугольника) будем составлять разные квадраты.
как гипотенуза исходного треугольника) будем составлять разные квадраты.
Один отдельно взятый квадратик (сторона 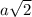 )
)
Квадрат из 4 квадратиков (сторона 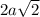 )
)
Квадрат из 9 квадратиков (сторона 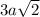 )
)
Квадрат из 16 и более квадратиков мы получить не можем, так как у нас есть только 12 квадратиков.
В этом случае, у нас получилось 3 различных квадрата, причем среди них нет квадратов, полученных в первой части решения.
Итого, 5+3=8 различных квадратов.
ответ: Г
20+5=25