10. У нас дано, что A⊂B.
Докажем, что (C\B)⊂(C\A).
Доказательство.
Пусть x∈C\B, тогда x∈C и x∉B,
если x∉B, то (т.к. A⊂B) x∉A, имеем
x∈C и x∉A, => x∈C\A.
чтд.
11. Доказательство "⇒".
Пусть у нас дано (A∪B = A∩B), докажем тогда, что A = B.
Доказательсво. Пусть x∈A, тогда x∈AUB, но т.к. A∪B = A∩B, то
x∈A∩B, и т.к. A∩B⊂B, имеем x∈B. Мы доказали сейчас, что А⊂B.
Теперь докажем, что B⊂A. Доказательство аналогичное:
пусть x∈B, => x∈A∪B, т.к. A∪B = A∩B, то x∈A∩B, т.к. A∩B⊂A, => x∈A.
Итак, B⊂A.
Т.к. A⊂B и B⊂A, ⇔ A = B. чтд.
Доказательство "<=".
Пусть у нас дано A = B, докажем тогда, что A∪B = A∩B.
Если A = B, то A∪B = B∪B = B, и A∩B = B∩B = B,
то есть A∪B = B = A∩B.
чтд.
12. Доказательство "=>"
Пусть у нас дано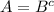 
, докажем тогда, что
(A∩B = ∅) и (A∪B = U).
Доказательство. 
это по определению есть U\B, где U - универсальное множество, то есть у нас дано
A = U\B, тогда
A∩B = (U\B)∩B,
если x∈A∩B, то x∈A и x∈B, то есть x∈U\B и x∈B, то есть
x∈U и x∉B, и x∈B,
x не может одновременно и принадлежать B и не принадлежать B, то есть такого x не существует, то есть x∈∅, мы доказали, что A∩B ⊂∅, но тогда A∩B = ∅.
теперь докажем, что A∪B = U,
Очевидно, что A∪B ⊂U,
докажем, что U⊂A∪B (при условии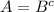 
).
если x∈U, тогда x∈B или x∉B,
( если x∉B, тогда x∈ ), имеем
x∈B или x∈
но т.к.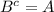 
имеем
x∈B или x∈A, то есть
x∈A∪B.
Мы доказали, что U⊂A∪B, и что A∪B⊂U (очевидное утверждение)
Итак, A∪B = U.
Доказательство "<=".
Пусть у нас дано: (A∩B = ∅) и (A∪B = U). Докажем, что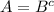
Доказательство. Пусть x∈A, при этом возможны два варианта:
x∈B или x∉B, то есть x∈B или x∈.
Если x∈B, тогда имеем x∈A∩B = ∅⊂
либо же x∈ и x∈A, ⇔ x∈A∩ ⊂,
то есть если x∈A => x∈
Пусть x∈, тогда x∈U\B, что значит x∈U и x∉B,
но т.к. U = A∪B, то имеем x∈A∪B и x∉B, то есть имеем
(x∈A или x∈B) и x∉B
если x∈A и x∉B, ⇔ x∈A\B ⊂ A, => x∈A,
если же x∈B и x∉B, то x∈∅ ⊂A, то есть x∈A,
итак ⊂A.
Мы доказали, что A⊂, и
.
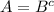чтд.
В решении.
Пошаговое объяснение:
На дворе была сделана цветочная клумба, состоящая из квадрата и четырёх полукругов.
Площадь клумбы приблизительно равна 2890 м².
Сколько метров декоративного забора необходимо вокруг клумбы? В расчётах использовано округлённое значение π≈3.
Решение.
Площадь клумбы состоит из квадрата и четырёх полукругов, что равно сумме площадей 2 кругов и 1 квадрата.
х - длина стороны квадрата.
R круга = D/2 = х/2 = 0,5х.
S круга = πR²
S квадрата = х².
По условию задачи уравнение:
2 * S круга + S квадрата = 2890
2 * πR² + х² = 2890
2 * 3 * (0,5х)² + х² = 2890
6 * 0,25х² + х² = 2890
1,5х² + х² = 2890
2,5х² = 2890
х² = 2890/2,5
х² = 1156
х = √1156
х = 34 (м) - длина стороны квадрата.
1. Какова длина стороны квадрата? 34 м.
2. Какова длина радиуса полукругов? 17 м.
34 : 2 = 17 (м).
3. Какова длина декоративного забора? 204 м.
Длина забора равна длине окружности 2 кругов (в клумбе 4 полукруга).
Формула длины окружности:
Р = 2πR
2 * 2 * π * R = 4*3*17 = 204 (м).
Разница в начислении по сравнению с линейным методом состоит в том, что в линейном методе амортизации каждый месяц будет одна и та же, а в уменьшаемого остатка начисление амортизации по окончании года использования идет с остаточной стоимости:
400 000*20%=80 тысяч начислена амортизация в 1ый первый год использования
400 000-80 000=320 000 -ост.ст-ть на начало второго года
320 000*20%=64 000 руб. начислена амортизация во 2 год
320 000-64 000=256 000 - ост.ст-ть на начало 3го года
256 000*20%=51 200 - начислена амортизация в 3ий год
256 000-51 200=204 800 -ост.ст-ть ОФ на начало 4го года
204 800*0,2=40 960 - начислена амортизация в 4ый год
204 800-40 960=163 840 руб. -ост.ст-ть на начало 5го года
163 840*0,2=32 768 -начислена амортизация в 5ый год
Остаточная стоимость на конец 5 года=163 840-32 768=131 072
Итого начислено амортизации:
84 000+64 000+51 200+40 960+32 768=272 928