Площадь фигуры, ограниченной данными линиями
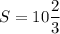ед.²
Пошаговое объяснение:
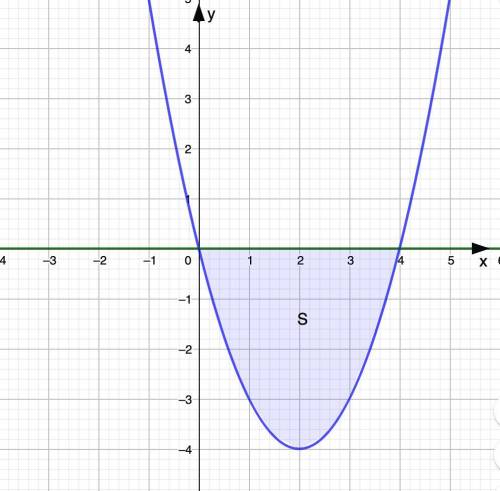
Надо вычислить площадь фигуры, ограниченной линиями:
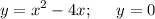
1. Для того, чтобы вычислить площадь фигуры, надо построить эти графики и найти точки их пересечения:
Первый график - парабола, ветви вверх.
Второй график - это ось 0х.
Если у = 0, то
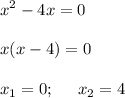
Формулы для вычисления площади фигуры, ограниченной линиями:
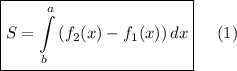
также нам понадобится формула Ньютона - Лейбница:
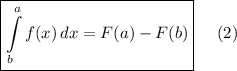
2. В нашем случае:
f₂(x) = 0 (ограничивает сверху); f₁(х) = х² - 4х (ограничивает снизу);
b = 0; a = 4.
Подставим эти значения в формулу (1) и с формулы (2) вычислим площадь фигуры:
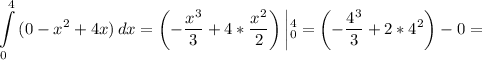
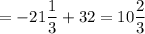(ед²)
⇒ площадь искомой фигуры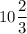 
ед.²
Пусть 1 - вся работа, тогда
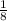- производительность ученика;
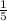- производительность мастера.
По условию подмастерье выполнил на 20% больше всей работы, чем мастер, значит,
(100% - 20%) : 2 = 40% работы выполнил мастер.
100% - 40% = 60% работы выполнил ученик.
Переведем проценты в дроби:
60% = 0,6 = 3/5 всей работы выполнил ученик;
40% = 0,4 = 2/5 всей работы выполнил мастер.
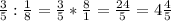часа работал ученик.
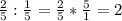часа работал мастер.
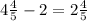ч на столько часов больше работал подмастерье, чем мастер.
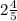ч = 2 ч 48 мин
ответ: на 2ч 48 мин. больше работал подмастерье, чем мастер.
КЕ= (2 2/3 *х) см
ДЕ=33 см
х+ 2 2/3*х=33
3 2 /3 *х = 33
11/3 *х =33
х= 33 :11/3 = 33/1 *3/11 =3*3
х=9 см - отрезок ДК
9 * 8/3 = 9*8/1*3=3*8 =24 см - отрезок КЕ
Проверим: ДЕ= ДК+КЕ= 9+24=33 см
ответ: отрезок ДК=9 см, КЕ=24 см.