Дана функция y=x³ +12x²+45x+50.
1. Определить область определения функции:
ограничений нет, вся числовая ось: D(f) = R.
2. Исследовать функцию на четность не четность:
f(-x) = (-x)³ + 12(-x)² + 45(-x) + 50 = -x³ + 12x²- 45x + 50 ≠ f(x),
f(-x) = -(x³ - 12x²+ 45x - 50) ≠ f(x). Значит, функция общего вида.
3. Найти координаты точек пересечения графика функции с осями координат:
- с осью Оу при х = 0. у = 50.
- с осью Ох при у = 0.
Надо решить уравнение x³ + 12x²+ 45x + 50 = 0.
Находим корни этого уравнения среди множителей свободного члена.
50 = +-1*+-2*+-5*+-5.
При подстановке определяем: х = -2 и х = -5 (2 раза).
x³ + 12x²+ 45x + 50 = (х + 2)*(х + 5)*(х + 5) = 0. х = -2 и х = -5.
4. Исследовать функцию на непрерывность, определить характер точек разрыва функции, если они имеются; найти асимптоты кривой:
точек разрыва и асимптот функция не имеет.
5. Найти интервалы возрастания и убывания функции и ее экстремумы.
Производная равна 3x²+ 24x + 45 = 3(x²+ 8x + 15).
Приравниваем её нулю (множитель в скобках):
x²+ 8x + 15 = 0.
Д = 64 - 4*1*15 = 4. х = (-8 +- 2)/2 = -3 и -5.
Находим знаки производной на полученных промежутках.
х = -6 -5 -4 -3 -1
y' = 9 0 -3 0 24.
Переход с + на - это максимум (х = -5, у = 0), с - на + это минимум(х = -3, у = -4). На промежутке (-∞; -5) и (-3; +∞) функция возрастает, на промежутке (-5; -3) функция убывает.
6. Найти интервалы выпуклости вверх и выпуклости вниз; определить точки перегиба
: y'' = (3x²+ 24x + 45)' = 6x + 24 = 6(x + 4) = 0.
Точка перегиба х = -4, у = -2.
Находим знаки второй производной на полученных промежутках.
x = -5 -4 -3
y'' = -6 0 6.
Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый:
• Выпуклая на промежутке: (-∞; -4).
• Вогнутая на промежутке: (-4; +∞).
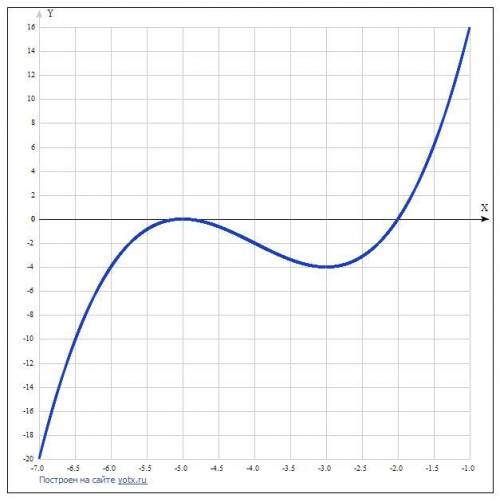
7. Построить график функции.
Таблица точек:
x y
-7.0 -20
-6.5 -10.1
-6.0 -4
-5.5 -0.9
-5.0 0
-4.5 -0.6
-4.0 -2
-3.5 -3.4
-3.0 -4
-2.5 -3.1
-2.0 0
-1.5 6.1
-1.0 16
График - в приложении.
 1. определить область существ" />
1. определить область существ" />
Надо определить функцию зависимости площади заданного прямоугольника от величины его сторон на катетах.
Пусть х - сторона на катете 2, а у - сторона на катете 4.
Из подобия треугольников с остатками сторон на катетах получаем:
у/(2 - х) = (4 - у)/х.
ху = (2 - х)(4 - у) = 8 - 4х - 2у + ху.
8 - 4х - 2у = 0.
Отсюда находим зависимость у от х: у = 4 - 2х.
Получаем формулу площади искомого прямоугольника:
S = xy = x(4 - 2x) = 4x - 2x².
Производная S' = 4 - 4x = 0. Это экстремум функции. х = 4/4 = 1.
Определяем знаки производной левее и правее точки х = 1.
х = 0,5 1 1,5
y' = 2 0 -2. Как видим, в точке х = 1 максимум.
у = 4 - 2*1 = 4 - 2 = 2.
ответ: вписанный прямоугольник имеет стороны 1 и 2.
2) Находим точки пересечения с осями:
х = 0 у = -3/5 это точка пересечения с осью у.
у = 0 надо числитель приравнять 0: 2х - 3 = 0 х = 3/2 это точка пересечения с осью х.
3) Исследуем функцию на парность или непарность:
Функция называется парной, если для любого аргумента с его областью обозначения будет f(-x)=f(x), или же непарной - если для любого аргумента с областью обозначения будет f(-x)=-f(x). К тому же, график парной функции будет симметричным относительно оси ординат, а график непарной - симметричным относительно точки (0;0).
Правда, чаще встречается название этих свойств функции как чётность и нечётность.
2*x - 3 -3 - 2*x ---------- = ---------- 1 1 (4*x + 5) (5 - 4*x) - Нет 2*x - 3 -3 - 2*x ---------- = - ---------- 1 1 (4*x + 5) (5 - 4*x) - Нет, значит, функция не является ни чётной, ни нечётной.
4) Исследуем функцию на монотонность: — это значит выяснить, на каких промежутках области определения функция возрастает, а на каких убывает.
Если производная положительна, то функция возрастает и наоборот.
Так как переменная в квадрате, то производная всегда положительна, а функция возрастающая на всей числовой оси (кроме х = -5/4).
5) Находим экстремумы функции:
Так как переменная находится в знаменателе, то производная не может быть равна нулю. Следовательно, функция не имеет ни максимума, ни минимума.
6) Исследуем функции на выпуклость, вогнутость:
Если вторая производная меньше нуля, то функция выпуклая, если производная больше нуля - то функция вогнутая.
Вторая производная равна
При x > (-5/4) функция выпуклая, при x < (-5/4) функция вогнута.
7) Находим асимптоты графика функции:
Горизонтальные асимптоты найдём с пределов данной функции при x->+oo и x->-oo 2*x - 3 lim ------- = 1/2 x->-oo4*x + 5 значит,уравнение горизонтальной асимптоты слева:y = 1/2 2*x - 3 lim ------- = 1/2 x->oo4*x + 5 значит,уравнение горизонтальной асимптоты справа:y = 1/2Наклонные асимптотыНаклонную асимптоту можно найти, подсчитав предел функции (2*x - 3)/(4*x + 5), делённой на x при x->+oo и x->-oo 2*x - 3 lim ----------- = 0 x->-oox*(4*x + 5) значит,наклонная совпадает с горизонтальной асимптотой справа 2*x - 3 lim ----------- = 0 x->oox*(4*x + 5) значит,наклонная совпадает с горизонтальной асимптотой слева
8) Можно найти дополнительные точки и построить график
График и таблица точек приведены в приложении.