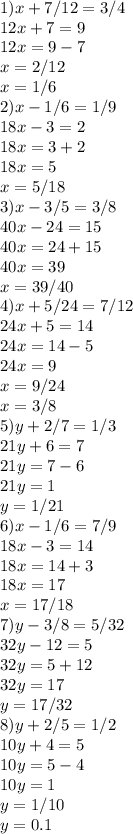
Пошаговое объяснение:
1вриант :
1) 10+8*2*2=72
2) 85
3) 20:2 +12-6 = 16
4) 23
5) 15 раз т.к 4*15 = 60
6) 4 раза.
7) 51:3=17 проверка: 17*3 = 51
8) 54:7= 7 (ост. 5)
9) 35 :8 = 4 (ост 3)
10) 2, 4, 1, 3.
11) х= 2
12) 24
13) 13 парт но ( 13-1 = 12(полных) но за одной партой 13той будит сидеть только 1 ученик)
2вриант:
1) 10*3*3-3 = 57
2) 90
3) 40:2+10-3 = 27 (тут у меня не получается)
4) 18
5) 13 раз т.к 5*13=65
6) 3 т.к 13*3=39
7) 19 проверка : 19*2=38
8) 59:8=7 (ост. 3)
9) 38:9=4 (ост. 2) т.к 9*4+2 = 38
10) 2, 4, 3, 1.
11) 42
12) 176
1)3*52=156
2)2*10=20
3) 156+20= 176
13) 14парт ( но 14-1=13(полных) но за 14 партой будит сидеть 1 ученик)
а) 27 б) 5
Пошаговое объяснение:
а) Можно было бы использовать готовые формулы, но покажу решение с объяснением.
По знанию языков сотрудники фирмы попадают в одну из восьми групп, которые не пересекаются друг с другом:
1. не знают ни одного языка
2. знают только английский
3. знают только немецкий
4. знают только французский
5. знают только английский и французский
6. знают только английский и немецкий
7. знают только французский и немецкий
8. знают все три языка
Определим из условия задачи численный состав этих групп.
Группа 1 по условию равна 0.
Группа 8 по условию равна 2.
Группа 5 равна 1 (три человека знают английский и французский, но из них двое входят в группу 8).
Группа 6 равна 4 - 2 = 2
Группа 7 равна 2 - 2 = 0
Группа 2 равна 17 - 1 - 2 - 2 = 12 (из всех знающих английский вычитаем тех, кто в дополнение к нему знает еще французский или немецкий или их оба)
Группа 3 равна 10 - 2 - 0 - 2 = 6
Группа 4 равна 7 - 1 - 0 - 2 = 4
Сложим количество людей во всех группах и получим численный состав фирмы:
0 + 2 + 1 + 2 + 0 + 12 + 6 + 4 = 27
б) Теперь Группа 1 = x, Группа 8 = 0
Группа 5 = 3
Группа 6 = 4
Группа 7 = 2
Группа 2 = 17 - 3 - 4 - 0 = 10
Группа 3 = 10 - 4 - 2 = 4
Группа 4 = 7 - 3 - 2 = 2
Получаем уравнение
x + 0 + 3 + 4 + 2 + 10 + 4 + 2 = 30
x = 5