Теорема Безу
Остаток от деления многочлена f(x) на двучлен (x - a) равен f(a)
Доказательство
f(x) = (x - a)·g(x) + r, где g(x) - частное, имеет степень на 1 меньше, чем f(x), а r - число (многочлен степени 0)
Тогда, подставляя x = a получаем:
f(a) = (a - a)·g(a) + r, то есть получаем f(a) = r, или r = f(a) - что и требовалось.
Теорема 2
x = a - корень f(x) ⇔ f(x) делится на (x - a)
Доказательство
из теоремы Безу получаем, что если f(a) = 0 (то есть a - корень f(x)) ⇒ f(x) = (x - a)·g(x) + 0 ⇒ f(x) при делении на (x - a) дает g(x) при 0-м остатке, а значит делится (x - a)
Обратно: раз f(x) делится на (x - a), значит остаток равен 0, а он по теореме Безу равен f(a), то есть a - корень f(x)
Пояснение:
S - площадь (прямоугольника),
a - длина (прямоугольника),
b - ширина прямоугольника.
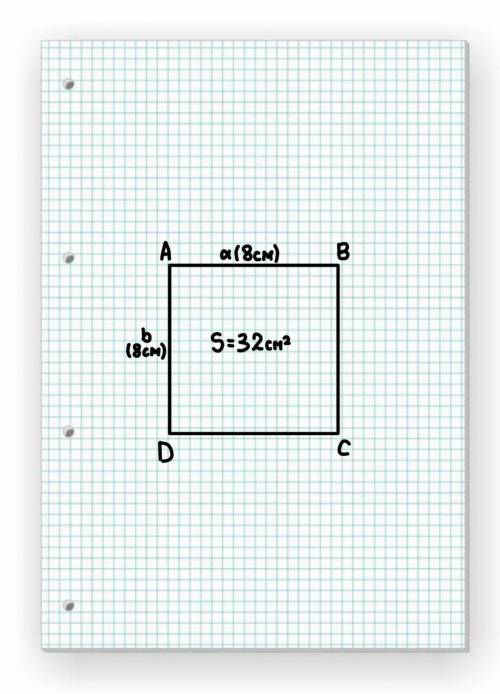
Чертёж:
См. прикреплённый файл.
Дано:
Прямоугольник ABCD,
S = 32 см²,
a = 8 см.
Найти:
b - ?
Задачу решим с уравнения.
S = 2 (a + b)
(S = 2a + 2b);
- 2b = 2a - S;
- 2b = 2 × 8 - 32;
- 2b = 16 - 32;
- 2b = - 16;
b = - 16 ÷ (- 2);
b = 8 см.
2b = S - 2a;
2b = 32 - 2 × 8;
2b = 32 - 16;
2b = 16;
b = 16 ÷ 2;
b = 8 см.
b = S - 2a / 2;
b = 32 - 8 × 2 / 2;
b = 32 - 16 / 2;
b = 16 / 2;
b = 16 ÷ 2;
b = 8 см.
Значит a = b (= 8см), из этого следует, что данный прямоугольник - квадрат.
ответ: ширина прямоугольника - 8 см.
_______________
Удачи Вам! :)
4 2/3 км = 14/3 км/ч скорость 1 пешехода
1 1/6 = 7/6 больше скорости 2 пешехода
14/3 : 7/6 = 4 км/ч скорость 2 пешехода
4 2/3 + 4 = 8 2/3 км/ч скорость удаления пешеходов друг от друга
8 2/3 = 26/3 км/ч
26 : 26/3 = 3 ч
ответ. Через 3 ч расстояние между пешеходами будет 26 км.