Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .
Находим векторы АВ, АС и АД.
Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.
Вектор АC={xC-xA, yC-yA, zC-zA} = (-6; 3; -4) =√61 ≈ 7,81025.
Вектор АD={xD-xA, yD-yA, zD-zA} = (-6; -1; -2) = √41 ≈ 6,40312.
Определяем векторное произведение АВ х АС.
i j k | I j
-4 2 -1 | -4 2
-6 3 -4 | -6 3 = -8i + 6j - 12k - 16j + 3i + 12k = -5i - 10j = (-5; -10; 0).
Далее находим смешанное произведение (АВ х АС) х АД.
(АВ х АС) = (-5; -10; 0),
АD = (-6; -1; -2),
(АВ х АС) х АД = 30 + 10 + 0 = 40.
Объем пирамиды равен (1/6) этого произведения:
V = (1/6)*40 = (20/3) куб.ед.
Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).
Площадь основания АВС равна половине модуля векторного произведения АВ х АС.
S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.
h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.
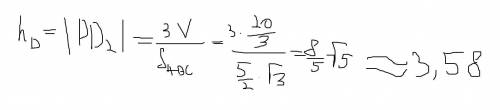
5/6 >5/8,_ 17/30< 2/3,_ 79/68 >5/113,_ 11/12 < 19/20,_ 2³/₁₆ < 2⁹/₁₆
Пошаговое объяснение:
1) При сравнении дробей с одинаковым числителем больше та дробь, знаменатель которой меньше.
5/6> 5/8 ( На чем больше частей делится что-то, тем меньше получится каждая часть).
2) 17/30 и 2/3 приведем к общему знаменателю:
17/30 <20/30 ( при сравнении дробей с равными знаменателями больше та, у которой больше числитель. Если что-то разделить на 30 частей , то 17 частей меньше. чем 20 таких же).
3) 79/68 и 5/113
Первое число - неправильная дробь, оно больше едииницы. Второе - меньше единицы. Поэтому
79/68 > 5/113
4) 11/12 и 19/20
Первому числу до целого недостает 1/12, второму 1/20.
Т.к. 1/12> 1/20, то 19/20>11/12 ( см. объяснение п. 1)
5) Из смешанных чисел с равной целой частью больше та, у которого больше дробная часть. 2=2, 9/16>3/16, поэтому 2 целых и 3/16 меньше, чем 2 целых и 9/16.