Было Стало
1-я ёмкость х + 3 х + 3 - 15
2-я ёмкость х х + 15
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Уравнение: (х + 3 - 15) · 2 = х + 15
(х - 12) · 2 = х + 15
2х - 24 = х + 15
2х - х = 15 + 24
х = 39 (л) - было во второй ёмкости
39 + 3 = 42 (л) - было в первой ёмкости
В первой ёмкости 42 литра кваса, а
во второй ёмкости 39 литров кваса.
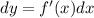 или
или 

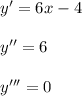


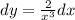
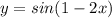




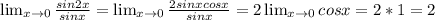
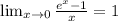
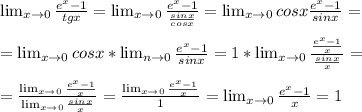
√2 *tq(180°+60°)*sin(360°-60°)*cos(7*180 °+45°)=√2 *tq60°*(-sin60°)*(-cos45°) =√2 *√3*(-(√3)/2)*(-√2)/2 =3/2 =1,5.
б) cos225°*sin300°+sin³45°*ctq150° =
cos(180°+45°)*sin(360° -60°)+sin³45°*ctq(180°-30°) =
-cos45°*(-sin60°+sin³45°*(-ctq30°) = (√2/2)*(√3/2)-(√2/2)³*√3 =
(√6)/4 - (√6)/4= 0.
в) cos1110°*sin1125° =cos(3*360°+30°)°*sin(3*360°+45°) =
cos30°°*sin45° =√3/2 *√2/2 = (√6)/4.
г) sin25°*sin85° +sin65°*sin5° =sin(90°-65°)*sin(90°-5°) +sin65°*sin5° =
cos65°cos5° +sin65°*sin5°=cos(65°-5°)=cos(60°) =0,5.
д) (sin26°*sin20° + cos26°*cos20°)/2cos6°=
(cos26°*cos20°+sin26°*sin20° )/2cos6 =
cos(26°-20°)/2cos6°= cos6°/2cos6° =0,5.
е) ! cos356° заменяю на cos354° ...
(cos66°*cos354°+sin186°*cos156°)/(sin36°*cos6° -sin126°*cos84°)=
(cos66°*cos6°+sin6°*sin66°)/(sin36°*cos6° -cos36°*sin6°) =
cos(66°-6°)/sin(36°-6°) =cos60°/sin30° =(1/2) / (1/2) =1.
ж) (3cosα -4sinα)/(4sinα +5cosα)= || cosα(3 -4tqα)/cosα(4tqα +5)||
(3 -4tqα)/(4tqα +5) =(3 -4*(-0,625))/(4*(-0,625)+5) =(3+2,5)(-2,5 +5) =
5,5/2,5 =11/5 =2,2.
* * * слишком много был * * *
От дед мороза !