Дано :
Четырёхугольник ABCD - равнобедренная трапеция (AB║DC, AD = BC).
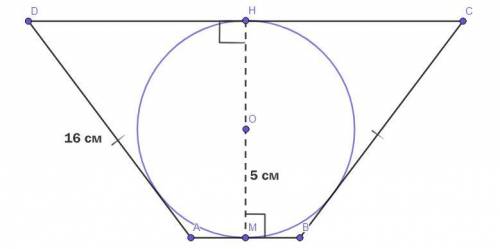
Окружность с центром О - вписанная в равнобедренную трапецию окружность.
ОМ - радиус окружности = 5 см.
AD = BC = 16 см.
Найти :
S(ABCD) = ?
Если в четырёхугольник можно вписать окружность, то суммы противоположных сторон равны.
Следовательно -
AD + BC = AB + DC.
Но так как -
AD = BC = 16 см.
Поэтому -
AD + BC = 16 см + 16 см = 32 см
AB + DC = 32 см.
Радиус вписанной в трапецию окружности равен половине высоты.
На чертёже НМ - высота ABCD, следовательно -
НМ = 2*ОМ
НМ = 2*5 см
НМ = 10 см.
Площадь трапеции равна произведению полусуммы оснований и высоты.
То есть -
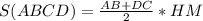
Теперь в формулу подставляем известные нам численные значения и считаем -
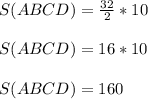
ответ : 160 (ед²).

приводим к общему знаменателю, т.е. к 14. Для этого 1/2 умножаем на 7 и получаем 1/2=7/14, а 6 3/7 умножаем на 2 и получаем 6 6/14
1/2+6 3/7=7/14+6 6/14=6 13/14