1) Уравнение стороны АВ:
, после сокращения на 10 получаем каноническое уравнение:
В общем виде х-у-3 = 0.
В виде уравнения с коэффициентом у = х-3.
2) уравнение высоты Ch.
(Х-Хс)/(Ув-Уа) = (У-Ус)/(Ха-Хв).
Подставив координаты вершин, получаем:
х + у + 1 = 0, или
у = -х - 1.
3) уравнение медианы am.
(Х-Ха)/(Ха1-Ха ) = (У-Уа)/(Уа1-Уа).
Основание медианы Am (Ха1;Уа1)= ((Хв+Хс)/2; (Ув+Ус)/2) =
= ((9-5)/2=2; (6+4)/2=5) = (2;5).
Получаем уравнение Am:
Можно сократить на 3:
y = 3x - 1.
4) Точка n пересечения медианы Аm и высоты Ch.
Приравниваем y = 3x - 1 и у = -х - 1.
4х = 0,
х = 0, у = -1.
5) уравнение прямой, проходящей через вершину C параллельно стороне AB.
(Х-Хс)/( Хв-Ха) = (У-Ус)/(Ув-Уа).
х - у + 9 = 0,
у = х + 9.
6) расстояние от точки С до прямой АВ.
Это высота на сторону АВ.
h = 2S/AB.
Находим стороны треугольника:
АВ = √((Хв-Ха)²+(Ув-Уа)²) = √200 ≈ 14.14213562,
BC = √((Хc-Хв)²+(Ус-Ув)²) = √200 ≈ 14.14213562,
AC = √((Хc-Хa)²+(Ус-Уa)²) = √80 ≈ 8.94427191.
Площадь находим по формуле Герона:
S = 60.
h = 2*60/√200 = 8.485281.
Имеем многочлен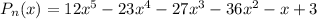 
Корнями многочлена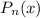 
называют корни уравнения
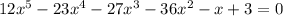
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена: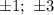 
Подставим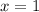 
в корень уравнения и получим:
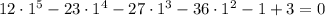
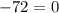— неправда
Подставим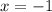 
в корень уравнения и получим:
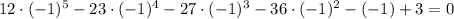
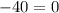— неправда
Подставим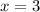 
в корень уравнения и получим:
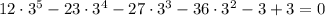
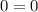— правда
Следовательно,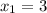 
— один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на 
(см. вложение).
После этого исходное уравнение можно записать разложив на множители:
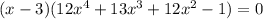
Решаем второе уравнение:
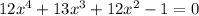
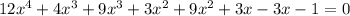
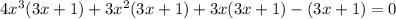
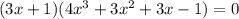
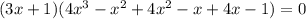
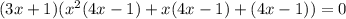
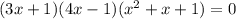
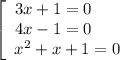
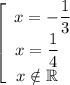
Рациональные корни: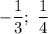 
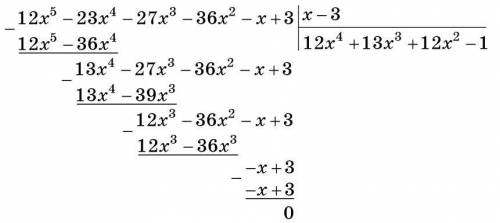
1)28:4=7
2)69-7=62
3)62-12=50
21+3*9-24=24
1)3*9=27
2)21+27=48
3)48-24=24
18:3*7+2=44
1)18:3=6
2)6*7=42
3)42+2=44
10*2+21:3=27
1)10*2=20
2)21:3=7
3)20+7=27