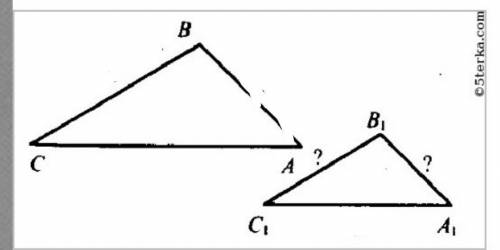
1 задача.
Треугольник ABC и A1B1C1 подобны, следовательно;
AB/A1B1=AC/A1C1=BC/B1C1
Возьмём большую сторону A1C1.
Значит выходит:
10/A1B1=15/12=12/B1C1 отсюда:
A1B1=10*12/15=8;B1C1=12*12/15=9.6
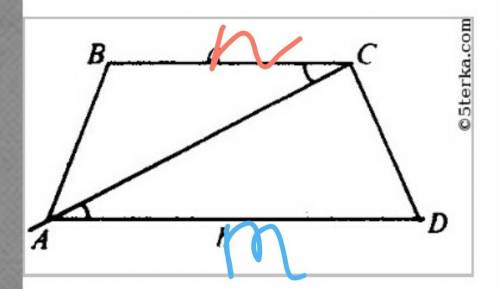
2 задача.
Треугольники ABC и ACD подобны;AD=m и BC=n.
Два треугольника подобны значит:AB/DC=BC/AC=AC/AD
AC²=AD*BC(свойства пропорции)
т.е. АС²=m*n
3 задача.
прямая пересекающия стороны в точках M и N
В треугольнике ABC и MNC;угол С общий.
угол М=угол А(потому что АВ||a)
Значит треугольник АВС и МNC подобны (по двух углам),отсюда:
BC/NC=AB/MN=AC/MC=4+5/5
Вот что выходит:AB/MN=9/5;BC/NC=9/5;AC/MC=9/5
MN=5/9AB=1.4×5=7см
NC=5/9BC=2×5=10см
MC=5/9AC=1.7×5=8.5см

Обозначим цифру десятков буквой х, цифру единиц буквой у.
Тогда число состоит из 10х и у
,Первое число будет 10х+у,
Во втором десятки и единицы поменялись местами.
Запишем уравнение, разности этих чисел:
10х+у - (10у+х)=45
9х - 9у =45
Так как сумма цифр 11, запишем второе уравнение:
х+у=11
Найдем из него значение у через х
у=11-х
9х - 9(11-х) =45
9х - 99+9х =45
18х=144
х=8
у=11-8=3
Заданное число 83
2)
Пусть производительность первой трубы х м³ в час, а второй у м³ в час
Тогда
3х-2у=8 м³
Вместе через две трубы выливается х+у м³ в час, а вся вода за 3⅓часа
Составим уравнение
120:(х+у)=3 ⅓
120 = 10 (х+у):3
360 = 10х +10у сократим на 10
36 = х + у
3х-2у=8
у=36-х подставим значение у в предыдущее уравнение
3х-2(36-х)=8
3х-72+2х =8
5х=80
х= 16 м³ в час
у=36-16=20 м³ в час
Проверка:
120:(20+16)=10/3 часа=3 ч 20 мин
3)
Пусть первая книга стоит х крон, а вторая у крон
Составим систему уравнений по условию задачи:
| х+ ⅔*у=171 уможим на 3 обе части уравнения
| ⅖ х+у=130 уможим на 5 обе части уравнения
получим:
|3х+2у=513
|2х+5у=650
Первое уравнение умножим на 2,5; получим
|7,5 х+5у=1282,5
|2х+5у=650
Вычтем из первого уравнения второе
5,5х=632,5 кроны
х=115 крон
2х+5у=650 подставим сюда значение х
230+5у=650
5у=420
у=84 кроны
ответ:115 крон и 84 кроны стоят книги