а).
Пусть требуемое в задаче возможно и в ящике есть 
("маленьких") фруктов меньше 
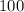грамм. Тогда ("больших") фруктов, чья масса больше
С одной стороны, масса всех фруктов равна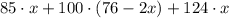 
, а с другой стороны - 
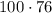. Но так как мы говорим об одной и той же группе фруктов, то:
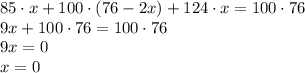
Но в задаче сказано, что "есть как минимум 
различных по массе фрукта". Но полученный в этом случае результат противоречит условию Из этого заключаем, что описанная ситуация невозможна.
ответ: нет, не может.
б).Пусть есть "маленьких" фруктов и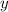 
"больших" (в этом случае "средних" фруктов будет 
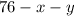). Точно также, как и в пункте, составим уравнение:
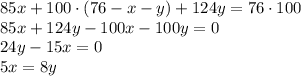
Мы получили очень интересный результат: в любом случае отношение количества "маленьких" и "больших" фруктов будет равно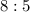 
.
Значит, так как и 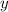обязательно должны быть натуральными, общее число "маленьких" и "больших" фруктов должно делиться на 
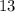. Такое общее число будет обязательно меньше или равно 
.
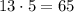Получается, что количество "средних" фруктов больше или равно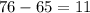 
. В ящике их 
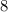уж никак не может быть.
ответ: нет, не может.
в).Так как в задаче сказано "найдите наибольшую возможную массу фрукта", то наверняка нужно считать массы фруктов целыми числами.
Если есть 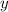"больших" фруктов и 
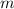- масса наибольшего,то, чтобы "понизить" значение среднего арифметического (и привести его в итоге к числу 
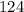), нужно массу остальных "больших" фруктов сделать как можно меньше - в районе 
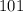грамма.
Поэтому:
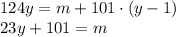
Как было фактически выяснено в пункте задачи, максимальное значение 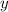равно 
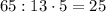(а 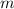максимальное при максимальном значении ).
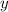Делаем вывод, что в этом случае:
.
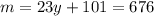Теперь проверим, что этот случай нам действительно подходит:
Есть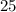
"больших" фруктов: масса 
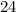из них равна 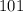, а масса 
составляет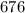 
граммов.Есть 
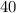"маленьких" фруктов: масса каждого - по 
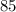граммов.И еще 
"средних" фруктов, ровно по 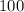граммов.Средняя масса "больших":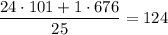 
.
Средняя масса "средних":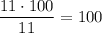 
.
Средняя масса "маленьких":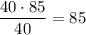 
.
Общая средняя масса: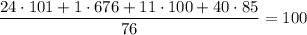 
.
Все сходится!
ответ: 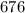граммов.
Пусть x овощей имеют массу меньше 1000, y - больше 1000, а z - ровно 1000.
а) Предположим, что да. Тогда справедливо уравнение:
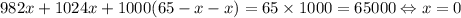, но x очевидно не может быть нулем, т.к. среднее арифметическое больше нуля. Противоречие.
б) Предположим, что это возможно. Тогда x+y+13=65 ⇔ x+y=52. Аналогично строим уравнение: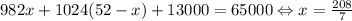 
, получили противоречие: x должно быть целым числом.
в) Понятно, что минимальная масса встречается только в группе, где расположены овощи массой меньше 1000 г. Обозначим массу самого легкого за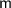 
; Пусть масса оставшихся в этой же группе овощей суммарно равна 
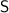; Тогда 
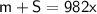; Заметим, что 
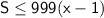; Поэтому 
(*);
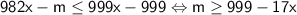Теперь рассмотрим уравнение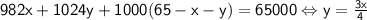 
, значит x кратно 4. Пусть 
;
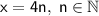Рассмотрим другое уравнение: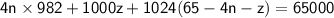 
; Отсюда получаем, что 
;
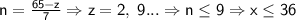Возвратимся к (*):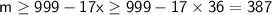 
; Приведем пример при котором осуществима оценка:
Пусть в первой группе 1 овощ весит 387 граммов, а остальные 35 весят по 999 граммов. Во второй группе 2 овоща весят по 1000 граммов. А в последней группе 27 овощей весят 1024 грамма.
ответ: а) нет
б) нет
в) минимально возможная масса - 387 граммов
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство. Рассмотрим два треугольника ABC и A1B1C1.
Пусть в этих треугольниках равны стороны AB и A1B1,
BC и B1C1,
а угол ABC равен углу A1B1C1.
Тогда треугольник A1B1C1 можно наложить на треугольник ABC так, чтобы угол A1B1C1 совпал с углом ABC.
При этом можно расположить треугольник A1B1C1 так, чтобы сторона А1В1 совпала со стороной АВ, а сторона B1С1 - со стороной BС. (В случае необходимости вместо треугольника A1B1C1 можно рассматривать равный ему "перевернутый" треугольник, т. е. треугольник, симметричный A1B1C1 относительно произвольной прямой .)
Тогда треугольники совпадут полностью, поскольку совпадут все их вершины.
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство. Пусть в треугольниках АВС и А 1 В 1 С 1 имеют место равенства
AB= A1B1,
ÐBAC = ÐB1A1C1,
ÐАВС= ÐА1В1С1.
Поступим так же, как и в предыдущем случае. Наложим треугольник А1В1С1 на треугольник АВС так, чтобы совпали стороны AB и A1B1 и прилегающие к ним углы. Как и в предыдущем случае, при необходимости треугольник А1В1С1 можно "перевернуть обратной стороной".
Тогда треугольники совпадут полностью. Значит, они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Доказательство. Пусть для треугольников ABC и A1B1C1
имеют место равенства АВ = А1В1,
ВС = В1С1,
СА = С1А1.
Перенесем треугольник А1В1С1 так, чтобы сторона А1В1 совпала со стороной АВ, при этом должны совпасть вершины A1 и A, B1 и B.
Рассмотрим две окружности с центрами в A и B и радиусами соответственно AC и BC.
Эти окружности пересекаются в двух симметричных относительно AB точках: C и C2. Значит, точка C1 после переноса указанным образом треугольника A1B1C1 должна совпасть либо с точкой C, либо с точкой C2.
В обоих случаях это будет означать равенство треугольников ABC и A1B1C1, поскольку треугольники ABC и ABC2 равны (эти треугольники симметричны относительно прямой AB.)