1. Метод исключения неизвестных.
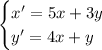
Продифференцируем первое уравнение:
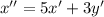
Подставим выражение для y':
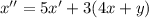
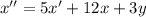
Из получившегося уравнения отнимем первое уравнение системы:
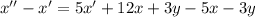
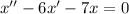
Составим характеристическое уравнение:
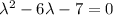
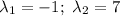
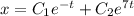
Найдем производную:
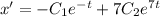
Выразим из первого уравнение системы у:
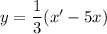
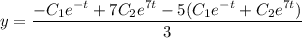
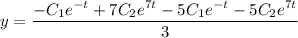
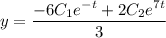
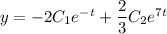
Общее решение:
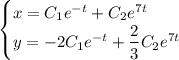
Находим решение задачи Коши:
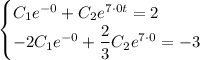
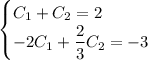
Первое уравнение домножим на 2:
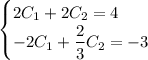
Сложим уравнения:
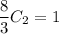
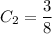
Выразим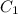 
:
Частное решение:
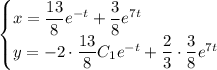
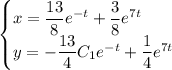
2. Метод характеристических уравнений (метод Эйлера).
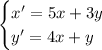
Матрица из коэффициентов при неизвестных:
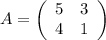
Характеристическая матрица:
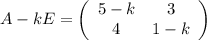
Характеристическое уравнение:
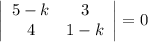
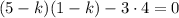
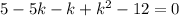
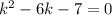
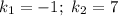
Общее решение:
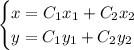
Ищем фундаментальную систему решений:
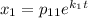
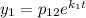
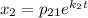
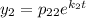
Для нахождения чисел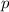 
составим систему:
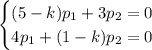
Для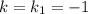 
:
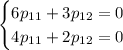
Оба уравнения дают:
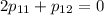
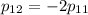
Найдем ненулевое решение. Пусть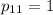 
. Тогда 
.
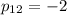Для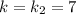 
:
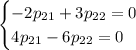
Оба уравнения дают:
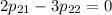
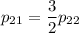
Найдем ненулевое решение. Пусть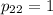 
. Тогда 
.
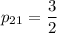Фундаментальная система решений найдена:
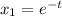
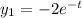
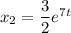
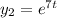
Общее решение:
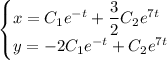
Находим частное решение:
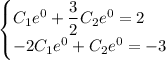
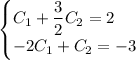
Первое уравнение домножим на 2:
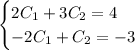
Сложим уравнения:
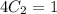
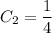
Выразим :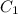
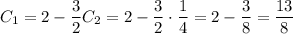
Частное решение:
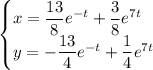
б) 3-х=1+х
3-1=х+х
2=2х
х=1
г) 5х-8=3х-8
5х-3х=8-8
2х=0
х=0
е) 5х-2(1/4)= 1/2х
5х-1/2х= 2(1/4)
4(1/2)х = 2(1/4)
х=2
з) 2х-3/5=3/4х-1/2х
2х-3/4х+1/2х= 3/5
1(3/4)х=3/5
х=3/10
№ 616
б) 12+3(х-1)=0
12+3х-3=0
9= - 3х
х= - 3
г) 1-5(2-3х)=6
1-10+15х=6
1-10-6= - 15х
- 15= - 15х
х=1
е) 5-2(3-х)=11
5-6+2х= 11
5-6-11= - 2х
-12= - 2х
х= 6
з) -3-3(3-2х)=1
-3-9+6х=1
-1-9-3= -6х
6х=13
Под буквой "з" опечатка или уравнение не имеет решения в целых числах
80 руб. - 100%
снижение цены - 15%
1 кг (после снижения) - ? руб.
Решение
1) 80:100%=0,8 (руб.) - составляет 1%.
2) 0,8*15=12 (руб.) - составляет 15 %.
3) 80-12=68 (руб.) - стали стоить помидоры после снижения цены.
ОТВЕТ: 68 рублей.
1) 100%-15%=85 % - составляет цена после понижения на 15 %.
2) Составим пропорцию:
80 руб. - 100%
х руб. - 85 %
80*85:100=6800:100=68 (руб.) - стали стоить помидоры после снижения цены.
ОТВЕТ: 68 рублей.