Периметр квадрата равен Р = 4а, где а - сторона квадрата
а = Р : 4 = 16 : 4 = 4 (см) - сторона квадрата.
Смотри построение на прикреплённом рисунке а)
1) Диагональ Ас соединяет вершины квадрата А и С и делит квадрат на два треугольника
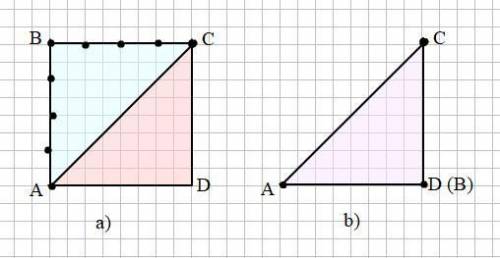
2) Перегните квадрат по диагонали АС, совместив точки В и D. (смотри рисунок b)
Очевидно, что треугольники АВС и АDС равны, значит равны и их площади.
3) Площадь квадрата АВСD
S = a² = 4² = 16 (cм²)
Площадь треугольника АВС равна половине площади квадрата, так как диагональ квадрата делит его на два равных треугольника
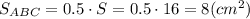
Пошаговое объяснение:
Открываем скобки в уравнении:
4 * 0,2х – 4 * 7 – 5 * 0,3х – 5 * 6 = 5;
0,8х – 28 – 1,5х – 30 = 5;
Скобки открыты. Перенесем слагаемые без переменной в правую часть уравнения, при этом меняем знак слагаемых на противоположные.
0,8х – 1,5х = 5 + 28 + 30.
Приведем подобные слагаемые в правой и левой частях уравнения, используя правило приведения подобных слагаемых.
х * (0,8 – 1,5) = 63;
- 0,7х = 63;
Разделим на – 0,7 обе части уравнения и тем самым найдем значение переменной х.
х = 63 : (- 0,7);
х = - 90.
Сделаем проверку:
4(0,2х – 7) – 5(0,3х + 6) = 5, х = - 90
4(0,2 * (- 90) – 7) - 5(0,3 * (- 90) + 6) = 5;
4(- 18 - 7) – 5(- 27 + 6) = 5;
4 * (- 25) – 5 * (- 21) = 5;
- 100 + 105 = 5;
5 = 5.
ответ: х = - 90.