Пошаговое объяснение:y'' = e2x
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2+0 r + 0 = 0
D=0*2 - 4·1·0=0 r1=0 r2=0
Корни характеристического уравнения:
Корень характеристического уравнения r = 0 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y1 = e0x
y2 = xe0x
Общее решение однородного уравнения имеет вид:
y1=C1 +C2x
Ci ∈ R
Рассмотрим правую часть:
f(x) = e2x
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = eax(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) - некоторые полиномы
имеет частное решение
y(x) = xkeax(R(x)cos(βx) + S(x)sin(βx))
где k - кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 0.
Следовательно, число α + βi = 2 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
y· = Ae2x
Вычисляем производные:
y' = 2·A·e2x
y'' = 4·A·e2x
которые подставляем в исходное дифференциальное уравнение:
y'' = (4·A·e2x) = e2x
или 4·A·e2x) = e2x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
1: 4A = 1
Решая ее, находим:
A = 1/4;
Частное решение имеет вид:
y2=1/4 *e2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y=y1+y2 =C1 +C2x +1/4 *e2x
Найдем частное решение при условии: y(0) = 3, y'(0) = 0
Поскольку y(0) = C1+1/4, то получаем первое уравнение:
C1+1/4 = 3
Находим первую производную:
y' = C2+e2x/2
Поскольку y'(0) = C2+1/2, то получаем второе уравнение:
C3+1/2 = 0
В итоге получаем систему из двух уравнений:
C1+1/4 = 3
C2+1/2 = 0
т.е.:
C1 = 11/4, C2 = -1/2
Тогда частное решение при заданных начальных условиях можно записать в виде:
y=11/4 - 1/2 *x +1/4*e2x
1) 4х²+11х-3=(х+3)(4х-1)
2) 5х²-8х+3>0
(5х-3)(х-1)>0
х∈(-∞;3/5)∪(1;+∞)
3) х⁴-5х²-6=0
х²=а
а²-5а-6=0
а1=-1; а2=6
х∉R; x1=-√6; x2=√6
ответ: x1=-√6; x2=√6
4) а12=а1+11d=-5+11×3=-5+33=28
S12=n(a1+an)/2 = 12(-5+28)/2=12×23/2=138
ответ: S12=138
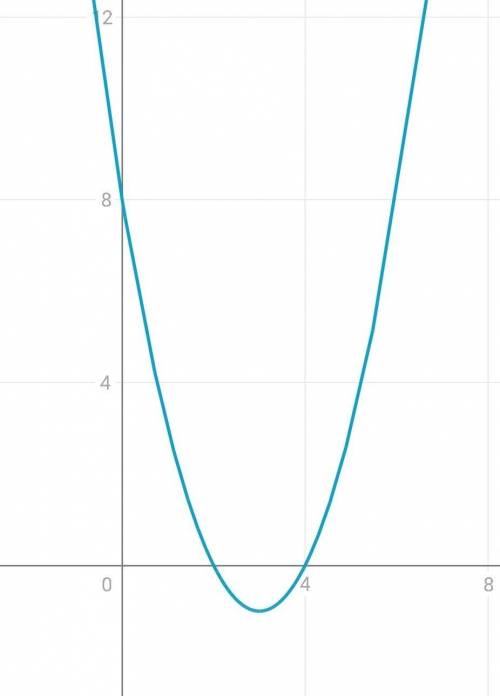
5) у=х²-6х+8
х²-6х+8=0
х1=2; х2=4
у=0²-6×0+8=8
График: парабола, ветки направлены вверх.
С осью Ох пересекается в точках 2 и 4.
С осью Оу пересекается в точке у=8
Ниже приведен график.
6) перевели минуты в часы: 54мин = 0,9ч
х - скорость первой группы
у - скорость второй группы
18=2×(x+y) => x+y=9
Составим систему:
{х+у=9
{18/х - 18/у = 0,9
Упростим второе уравнение, а из первого вытащим х:
{х=9-у
{18у-18х=0,9ху
Подставим значение Х во второе уравнение:
18у-18(9-у)=0,9у(9-у)
18у-162+18у-8,1у+0,9у²=0
0,9у²+27,9у-162=0 |:0,9
у²+31у-180=0
по т.Виета: у= -36 – посторонний корень; у=5
х=9-5=4
ответ: Скорость первой группы 4км/ч; скорость второй группы 5км/ч