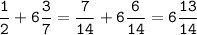
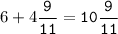
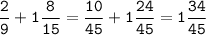
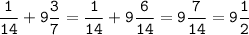
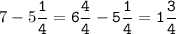
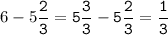
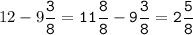
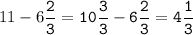
Найти наибольшее M и наименьшее m значения функции
f(x )=f(x) = x³- 3x²-9x+35 на отрезке на отрезке [-4;4] .
ответ: Д M = 40 ; m = -41 .
Пошаговое объяснение:
f '(x)=(x³- 3x²-9x+35) ' = 3x² - 6x-9 =3(x²-2x -3) .
Критические(стационарные) точки: f '(x)=0 ⇔3(x²-2x -3 =0) || 3≠0|| ⇔
x²-2x -3 =0 ⇒ x₁ = -1 ; x₂=3.
- - - - - -
f(x₁) =f(-1) = 1³- 3*(-1)²- 9*(-1)+35 = 40 ;
f(x₂)= f(3) =3³ - 3*3²- 9*3+35 =7 ;
f( - 4) =(-4)³ - 3*(-4)²- 9*(-4)+35 = - 41 ;
f(4) =4³ - 3*4²- 9*4+35 =17 .
M =max{40 ; 7 ; -41 ; 17} = 40 ; m =min{40 ; 7 ; -41 ; 17} = - 41 .
Д M = 40 ; m = -41 .
Обозначим попадание в цель первым стрелком – событие
A , вторым – событие B , промах первого стрелка – событие А ,
промах второго – событие В .
P(A) = 0,7; P(A) = 0,3; P(B) = 0,8; P(B) = 0,2.
Вероятность того, что первый стрелок попадет в мишень, а второй
– нет - равна
P(A)P(B) = 0,7 ×0,2 = 0,14
Вероятность того, что второй стрелок попадет в цель, а первый –
нет:
P(A)P(B) = 0,3×0,8 = 0,24
Тогда вероятность попадания в цель только одним стрелком равна
P = 0,14 + 0,24 = 0,38.
Тот же результат можно получить другим находим
вероятности того, что оба стрелка попали в цель и оба
промахнулись. Эти вероятности соответственно равны:
P(A)P(B) = 0,7 × 0,8 = 0,56; P(A)P(B) = 0,3× 0,2 = 0,06.
Тогда вероятность того, что в цель попадет только один стрелок,
равна:
P = 1− 0,56 − 0,06 = 0,38