Наибольшее возможное значение выражения (F+O+X+E)*(F*R*D*D) = 236196. Прилагаю небольшой скрипт на Python. Простенькая задачка на корректную организацию перебора с использованием вложенных циклов:
max_num = 0
for f in xrange(10):
for o in xrange(10):
for x in xrange(10):
for e in xrange(10):
for r in xrange(10):
for d in xrange(10):
b = f*r*d*d
if b == 0:
continue
num = (f + o + x + e) * b
if num > max_num:
max_num = num
print "Maximum value of (F+O+X+E)*(F*R*D*D) is: %i" % max_num
Решение можно получить гораздо проще, если догадаться, что наибольшее значение выражения достигается, когда сумма F+O+X+E и произведение F*R*D*D являются максимальными. Это одновременно происходит, когда все цифры равны 9: (9+9+9+9)*9*9*9*9 = 236196
Пошаговое объяснение:


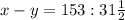 :
: 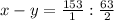

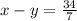
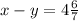
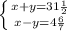
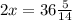
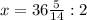
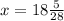

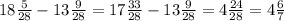


 и
и 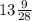 .
.