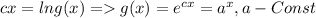первый случай
|x+2+(−x−4)|−8=x, -х-4>=0
|x+2−x−4|−8=x, -х>=4
|−2|−8=x, х<=-4
2−8=x, х<=-4
х=-6, х<=-4
х=-6
второй случай
|x+2-(−x−4)|−8=x, -х-4<0
|x+2+x+4|−8=x, -х<4
|2x+6|−8=x, х>-4
первый подслучай
2x+6−8=x, х>-4, 2x+6>=0
2x−2=x, х>-4, x+3>=0
x=2, х>-4, x>=-3
второй подслучай
-(2x+6)−8=x, х>-4, 2x+6<0
-2x-6−8=x, х>-4, x+3<0
-3x=14, х>-4, x<-3
x=-14/3, х>-4, x<-3 - между прочим, не корень
большее из чисел -6 и 2 - число 2
ответ: 2
2. 
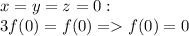
Введем функцию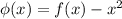 
Тогда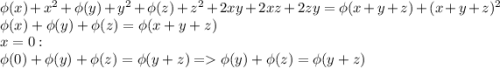 
Т.е.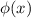 
удовлетворяет функциональному уравнению Коши. А значит 
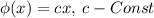(в классе непрерывных функций других решений нет).
Тогда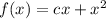 
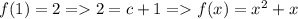
3. Если в область определения входит 0, то
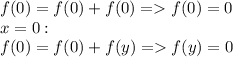
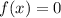- единственное решение.
Пусть функция не определена в 0.
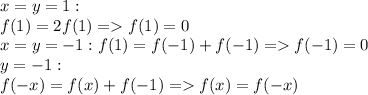
Тогда для удобства ограничим область определения функции положительными числами (а при отрицательном значении аргумента функция примет модуль числа)
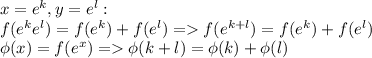
Т.е. 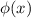удовлетворяет функциональному уравнению Коши. А значит 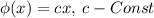(в классе непрерывных функций других решений нет).
![f(e^x)=cx=[x=lnt]=f(t)=c\cdot lnt](/tpl/images/1056/8113/e7416.png)
Вернем исходную область определения функции, заменив переменную на ее модуль: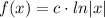 
4. Очевидно, что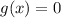 
- одно из решений.
Пусть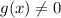 
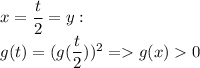
Значит можно логарифмировать
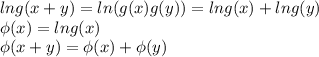
Т.е. 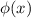удовлетворяет функциональному уравнению Коши. А значит 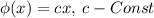(в классе непрерывных функций других решений нет).
