S(ABC) = 40 см²
Пошаговое объяснение:
Дано:
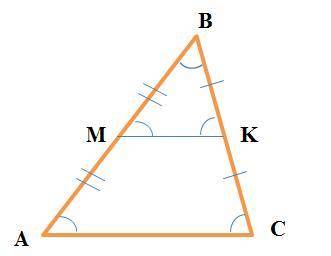
В ΔABC (см. рисунок)
MK - средняя линия
Площадь S(MBK)=10 см²
Найти: S(ABC)
Решение.
MK - средняя линия и поэтому параллельна к основанию AC и ∠BAC=∠BMK и ∠BCA=∠BKM. Отсюда, треугольники ABC и MBK подобны по I признаку (по 2 углам): ∠BAC=∠BMK и ∠BCA=∠BKM.
Так как AB=2·MB, то коэффициент подобия равен k=AB:MB=2·MB:MB=2.
Воспользуемся свойством подобных треугольников:
Отношение площадей подобных треугольников равно квадрату коэффициента подобия!
Тогда
S(ABC):S(MBK)=k²=2²=4.
Отсюда
S(ABC)=4·S(MBK) = 4·10 см² = 40 см².