Уравнение трехзначного числа: 100a+10b+c, где a - число сотен, b - число десятков и x - число единиц. Сумма цифр такого числа равна a+b+c. 100a+10b+c+7 (a+b+c) = 1000 107a+17b+8c=1000. При b=c=0 получим 107a=1000, и тогда a=9. При b=c=9 получим 107a+153+72=1000; 107a=775, получается a=7. При a=7: 749+17b+8c=1000; 17b+8c=251; При b=c=9 получим 225≠251, следовательно, a≠7. При a=8 получаем 856+17b+8c=1000; 17b+8c=144; b = (144-8c) / 17, c в промежутке между 0 и 9. Так как это число натуральное, подбираем такое с, чтобы дробь была целой. При с=1 и получаем b = 8. Это число 887. ответ: 887.
Пошаговое объяснение:
Дано: y = -x³ + 1
D(y) = [-2;0] - область определения.
Пошаговое объяснение:
1. Гладкая непрерывная функция - график в приложении.
2. Нуль функции: Y(x) = 0, x = 1.
3. На D(y) - убывает.
4. Максимум: Y(-2) = 9, минимум: Y(0) = 1.
5. Площади - интеграл функции. a = 0, b = - 2
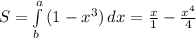
Именно такая запись мне нравится при интегрировании функций - степень увеличивается (в числителе), а знаменателе - значение этой степени.
6. Вычисляем на границах интегрирования
S(0) =0, S(-2) = -2 - 16/4 = - 6. S = 0 - (-6) = 6 - площадь - ответ.
![Y=-x³+ 1 [-2; 0] исследовать функцию построить её график найти наибольшее и наименьшее значения функ](/tpl/images/0984/1994/edd2b.jpg)