1) Дать определение: число a больше числа b
a > b, ели a − b > 0
Число a больше числа b, если разность этих чисел положительна.
2) Сравнить:
а)
8/11 и 9/13
Вычтем из первого числа второе:
 и 0
и 0
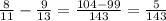
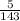 и 0
и 0
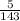 > 0
> 0
Значит, 
б)
a²+16 и 8a
Вычтем из первого выражения второе:
a²−8a+16 и 0
(a−4)² и 0
по определению, вырежение в квадрате всегда дает число неотрицательное, то есть (a−4)²≥0
(a−4)² = 0, если a = 4
(a−4)² > 0, если a ≠ 4
Значит, a² + 16 > 8a, если a ≠ 4; и a²+16 = 8a, если a = 4.
3) Доказать неравенство:
(a−3)(a+11) < (a+3)(a+5)
a²+11a−3a−33 < a²+5a+3a+15
Вычтем из первого выражения второе:
a²+11a−3a−33−a²−5a−3a−15 и 0
−48 и 0
Значит, (a−3)(a+11) < (a+3)(a+5), что и требовалось доказать.
4) Сравнить числа а и b, если верно неравенство: 3a−3b ≥ 1
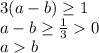
5) Оценить величину: 5а−2, если 1,1 < а ≤ 1,2
Умножим все части неравенства на 5:
5·1,1 < 5a ≤ 5·1,2
5,5 < 5а ≤ 6
Вычтем из всех частей неравенства 2:
5,5−2 < 5а−2 ≤ 6−2
Получаем:
3,5 < 5а−2 ≤ 4
1) 3cos2a−4sin2a=3cos2a−4(1−cos2a)=7cos2a−4T.k. −1≤cos a≤1, mo 0≤cos2a≤1 =>−4≤7cos2a−4≤3
-4 - наименьшее значение
3 - наибольшее значение.
\begin{lgathered}2)\ 2sin^2a +3tg\ a*ctg\ a =2sin^2a +3\\ T.k.\ -1 \leq sin\ a \leq 1,\ mo\ 0 \leq sin^2a \leq 1\ => \\ 3 \leq 2sin^2a+3 \leq 5\end{lgathered}2) 2sin2a+3tg a∗ctg a=2sin2a+3T.k. −1≤sin a≤1, mo 0≤sin2a≤1 =>3≤2sin2a+3≤5
3 - наименьшее значение
5 - наибольшее значение.
\begin{lgathered}3)\ 3cos^2a-4sin\ a=3(1-sin^2a)-4sin\ a=-3sin^2a-4sin\ a+3 \\ \Pi ycmb\ sin\ a=t,\ -1 \leq t \leq 1\ =>\\ f(t)=-3t^2-4t+3,\ t \in [-1;1]\\ f'(t)=-6t-4\\ f'(t)=0\ => -6t-4=0\ npu\ t=-\frac{2}{3}\\ f(-\frac{2}{3})=-3(-\frac{2}{3})^2-4(-\frac{2}{3})+3=4\frac{1}{3}\end{lgathered}3) 3cos2a−4sin a=3(1−sin2a)−4sin a=−3sin2a−4sin a+3Πycmb sin a=t, −1≤t≤1 =>f(t)=−3t2−4t+3, t∈[−1;1]f′(t)=−6t−4f′(t)=0 =>−6t−4=0 npu t=−32f(−32)=−3(−32)2−4(−32)+3=431
\begin{lgathered}f(-1)=-3(-1)^2-4(-1)+3=2\\ f(1)=-3*1^2-4*1+3=-4\end{lgathered}f(−1)=−3(−1)2−4(−1)+3=2f(1)=−3∗12−4∗1+3=−4
-4 - наименьшее значение
4\frac{1}{3}431 - наибольшее значение.
НОЗ (9, 12, 8 и 24) = 72 - общий знаменатель
72 : 9 = 8 - доп.множ. к 4/9 = (4*8)/(9*8) = 32/72
72 : 12 = 6 - доп.множ. к 10/12 = (10*6)/(12*6) = 60/72
72 : 8 = 9 - доп.множ. к 4/8 = (4*9)/(8*9) = 36/72
72 : 24 = 3 - доп.множ. к 14/24 = (14*3)/(24*3) = 42/72
В порядке убывания: 10/12 > 14/24 > 4/8 > 4/9.