7
Пошаговое объяснение:
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть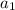 
- изначальное число и 
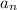- сумма цифр числа 
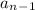. Пусть остаток при делении на 9 у числа 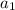- r, тогда и у числа 
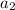остаток при делении на 9 тоже r. Но тогда и у чисел 
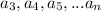остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа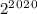 
. А он такой же, как у числа 
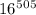, и такой же, как у числа 
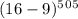, и такой же, как у числа 
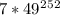, а он такой же, как у числа 
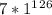, а это равно 7.
1. 2/5
2. 0,36
Пошаговое объяснение:
Задание 1.
Белых - 6 шаров
Черных - 10 шаров
В полоску - 14 шаров
В клетку - 10 шаров
Всего: 6+10+14+10 = 40 шаров
Одноцветных шаров (белые и черные шары): 6+10 = 16
Событие А - извлечение одного одноцветного шара
Вероятность Р(А) = 16/40 = 2/5
Задание 2.
Всего: 100 билетов
20 руб. - 9 билетов
15 руб. - 12 билетов
10 руб. - 15 билетов
2 руб. - 26 билетов
Событие А - " на купленный билет будет получен выигрыш не меньше 10 руб."
Т.е. выигрыш может составить 10 руб. или 15 руб. или 20 руб.
Р(А) = (9+12+15)/100 = 36/100 = 0,36
