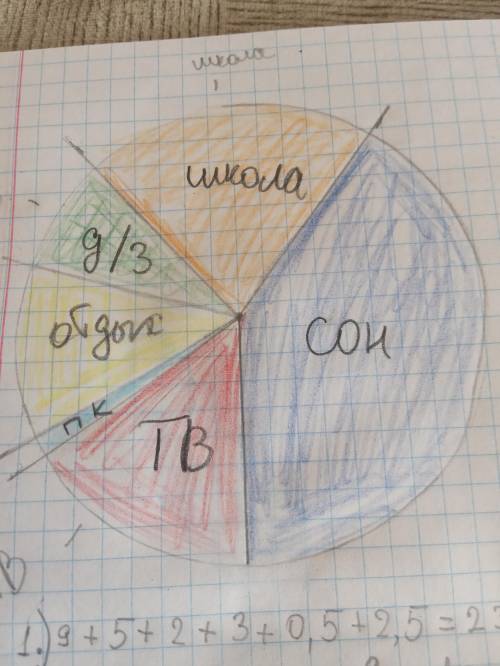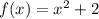Нужен к завтрему доклад ,,волейбол.правила игры.жесты судей.". кратко! !

👇

Ответ:

maks7388

29.01.2022

Волейбол — неконтактный, комбинационный вид спорта, где каждый игрок имеет строгую специализацию на площадке. Важнейшими качествами для игроков в волейбол являются прыгучесть для возможности высоко подняться над сеткой, реакция, координация, физическая сила для эффективного произведения атакующих ударов. Цель игры получить очко, забив мяч на противоположную сторону или заставить противника ошибиться. Разрешение на подачу; Подающая команда; Смена сторон площадок; Перерыв; Замена. Круговое движение предплечий вокруг друг друга; Предупреждение или замечание за неправильное поведение (показать желтую карточку для предупреждения, красную карточку для замечания); Удаление. Показать обе карточки в одной руке; Дисквалификация. Показать обе карточки в разных руках; Конец партии или встречи. Скрестить предплечья с вытянутыми кистями перед грудью; Мяч не подброшен при ударе на подаче. Поднять вытянутую руку с ладонью, обращенной вверх

4,5(1 оценок)

Открыть все ответы

Ответ:

Kotik77789

29.01.2022

Пусть функция f(x)=x^2+2

определена на множестве E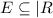 $E\subseteq |R$
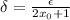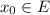Пусть $\delta=\frac{\epsilon}{2x_0+1}$ где $x_0 \in E$ .
Понятно, что для любого

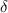на области $\delta$ от x_0

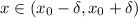(то есть: $x \in 
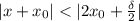(x_0-\delta,x_0+\delta)$ ) выполняется $|x+x_0|<|2x_0+ \frac{\delta}{2}|$ .
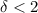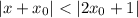Следовательно, для $\delta<2$ , выполняется |x+x_0|<|2x_0+1|

.

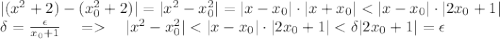
$|(x^2+2)-(x_0^2+2)|=|x^2-x_0^2|=|x-x_0|\cdot|x+x_0| < |x-x_0|\cdot|2x_0+1| \\
\delta= \frac{\epsilon}{x_0+1} \ \ \ = \ \ \ |x^2-x_0^2|< |x-x_0|\cdot|2x_0+1|<\delta|2x_0+1|=\epsilon$

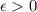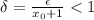Получили, что для любого $\epsilon 0$ есть $\delta=\frac{\epsilon}{x_0+1}<1$ , на области которой выполняется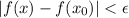 $|f(x)-f(x_0)|<\epsilon$
(Проще говоря:
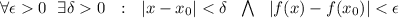$\forall
 \epsilon0 \ \ \exists\delta0 \ \ : \ \ |x-x_0|<\delta \ \ 
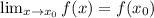\bigwedge \ \ |f(x)-f(x_0)|<\epsilon$ ). Следовательно - $\lim_{x 
\to x_0} f(x)=f(x_0)$ .
Что и требовалось доказать.
Для x_0=-1

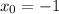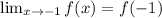нужно отдельно доказать предел $\lim_{x \to -1} f(x)=f(-1)$ .

Теперь в чём проблема самого вопроса: мы только что доказали непрерывность функции на любом подмножестве

. Но! Множество натуральных чисел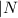

тоже подмножество

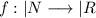, значит $f:|N \longrightarrow |R$ тоже непрерывна, получается - доказали что

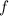непрерывна на области определения? Известно, что 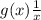$g(x) \frac{1}{x}$ тоже непрерывна на области определения, но

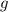, понятное дело, не определена на

!
Потому вопрос, ИМХО, поставлен не верно (претензия не к тебе, а скорее к преподавателям твоим). Правильно задать вопрос указывая то множесто точек, которое интересует: к примеру "непрерывна на

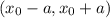" или, "непрерывна на отрезке (x_0-a,x_0+a)

"...
Тем более, что есть понятие "равномерная непрерывность" - свойство области, а не так, как "непрерывность" - свойство точки. Отсюда и непонимание.
А то получается: спрашивают об области, а проверяют точку.
Будут вопросы - пиши.

P.S. Исправил ошибки в наборе символов. Текста много :)

4,7(52 оценок)

Ответ:

sinethu

29.01.2022

Привет)

1. 9+5+2+3+0,5+2,5=23 ч - всего в распорядке дня.

2. 360°:23≈15,6° - 1 ч на круге

(0,5 ч =7,8°)

Теперь каждое значение (сон, школа и т.д.) умножаем на 15,6° и тем самым находим, сколько градусов будет на круговой диаграмме.

9•15,6=140,4° - сон

5•15.6=78° - школа

2•15.6=31,2° - д/з

3•15.6=46,8° - отдых

0.5•7.8=3.9° - работа с ПК

2.5•(7.8+15.6)°=58,5° - просмотр передач

Чтобы проверить, правильно ли вышло, мы должны сложить все значения и должно получиться 360°. У нас во втором действии приблизительно, поэтому будет не 360, а приблизительно.

140.4+78+31.2+46,8+3.9+58.5=358.8°