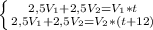
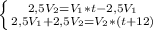
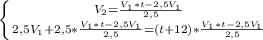
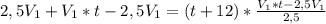
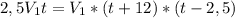; V(1) сокращаем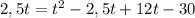
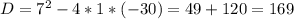
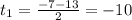ч - не подходит, время не может быть отриц.
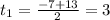ч - время мотоциклиста потраченное на весь путь из А в В
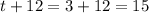ч - время велосипедиста потраченное на весь путь из В в А.
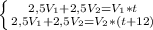
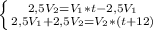
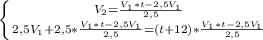
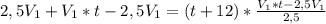
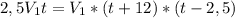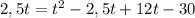
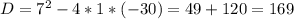
; V(1) сокращаем 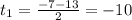ч - не подходит, время не может быть отриц. 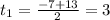ч - время мотоциклиста потраченное на весь путь из А в В 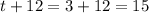ч - время велосипедиста потраченное на весь путь из В в А.
(4 + 1,8) + 2,2 = 4 + (1,8 + 2,2) = 4 + 4 = 8
1,6 + (5 + 3,4) = (1,6 + 3,4) + 5 = 5 + 5 = 10
(2,41 + 13) + 4,59 = (2,41 + 4,59) + 13 = 7 + 13 = 20
0,3 + (1,7 + 2,5) = (0,3 + 1,7) + 2,5 = 2 + 2,5 = 4,5
(3,8 + 6) + 4,2 = (3,8 + 4,2) + 6 = 8 + 6 = 14
12,25 + (8 + 3,75) = (12,25 + 3,75) + 8 = 16 + 8 = 24
8,3 + (2,7 + 8) = (8,3 + 2,7) + 8 = 11 + 8 = 19
10,2 + (1,7 + 4,8) = (10,2 + 4,8) + 1,7 = 15 + 1,7 = 16,7
(46,3 + 18) + 4,7 = (46,3 + 4,7) + 18 = 51 + 18 = 69