Стрелок два раза попадает и один раз промахнулся. Данное событие можно расписать в следующем виде:
1) Попал при первом и втором выстреле, промахнулся при третьем выстреле
2) Попал при первом и третьем выстреле, промахнулся при втором выстреле
3) Попал при втором и третьем выстреле, промахнулся при первом выстреле
Вероятность того, что стрелок при первом и втором выстреле попал, а при третьем выстреле промажет, равна
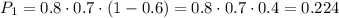
Вероятность того, что стрелок при первом и третьем выстреле попадет, а при втором выстреле промажет, равна
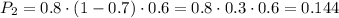
Вероятность того, что стрелок при втором и третьем выстреле попадет, а при первом выстреле промажет, равна
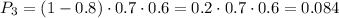
Искомая вероятность, по теореме сложения: P = P₁+P₂+P₃ = 0.452
2) Найти вероятность того, что стрелок получит хотя бы одно попадание.
Найдем сначала вероятность того, что стрелок ни разу не попадет в мишень
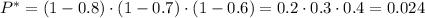
Тогда вероятность того, что стрелок имеет хотя бы одно попадания(вероятность противоположного события), равна
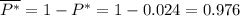
ответ:Первая задача решается по формуле Байеса
0.2*0.85/(0.3*0.8+0.5*0.9+0.2*0.85) - искомая вероятность
Вторая задача - по формуле полной вероятности
0.3*0.4+0.5*0.3+0.2*0.2 - искомая вероятность
2)Решение.
a) Вероятность, что первый шар белый Р=5/9
Осталось 4 белых, всего 8 шаров, вероятность вытащить второй белый = 4/8=1/2
Р=5/9*1/2 = 5/18 =0,28
б) Р=4/9 * 3/8 = 1/6
в) Вероятность, что первый черный, а второй белый Р=4/9 * 5/8 = 5/18
Вероятность, что первый белый, а второй черный Р=5/9 * 4/8 = 5/18
Окончательно, вероятность, что 1 белый и один черный Р=5/18 + 5/18 = 10/18 = 5/9
3)Найдите вероятность наступления ровно 3 успехов в 8 испытаниях Бернулли с вероятностью успеха p =1/2
Решение. Вероятность успеха =1/2, а вероятность не успеха равна 1-1/2=1/2.
Р8(3) = С83*(1/2)3*(1/2)5 = 8!/(3!*5!) * (1/2)8 = 8*7/256 = 7/32 ≈0,219
Пошаговое объяснение:100%правильно лайк поставьте а то жаловатся буду
sin²x+cos²x=1
sin²x+(3/5)²=1, sin²x=1-9/25. sinx=4/5
sin2x=2sinx*cosx
sin2x=2*(3/5)*(4/5)
sin2x=24/25