скорее всего если вы пятом классе, вы решаете в столбик , поэтому некоторые решения , которые нельзя посчитать устно, я прикреплю в фото.
Задание 1
5,006
5,020
5,028
5,065
5,650
Задание 2
а) 54,36 • 0,1= 5,436
b) 93,5 • 1000= 93500
c) 42,5 • 7,2 = 306
d) 485,55 : 100 = 4,8555
e) 32,12 : 0,01 = 3212
f) 29,4 : 7,5 = 3,92
Задание 3
Пусть первый сосуд вмещает х+3,6 л , второй х л, поскольку вместе их вместимость 12,8 л,
составим уравнение:
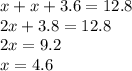
(л) — второй сосуд
4,6+ 3,6 = 8,2 (л)
ответ: 8,2 л — вместимость большего сосуда.
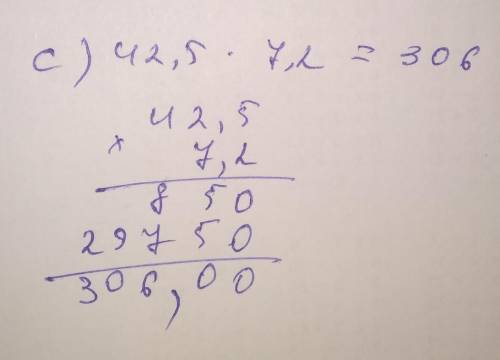
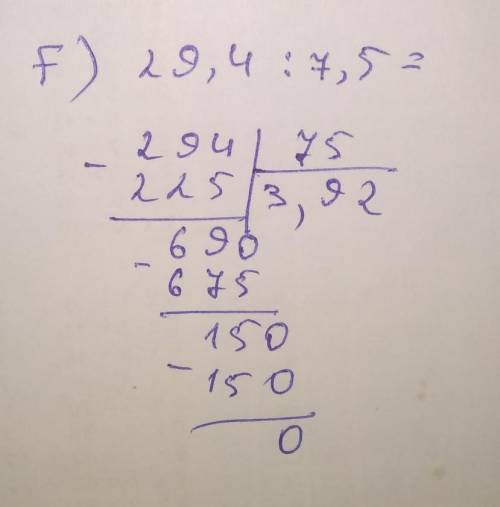
№ 4. x ≤ 0.75
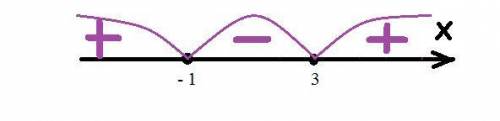
№ 5. ( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пошаговое объяснение:
№ 4. 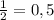
Тогда выражение имеет вид:
(0,5)^ (2*x) ≥ (0.125) ^ (1/2)
(0.5) ^ (2*x) ≥ ((0.5)^3)^(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3*(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3/2)
(0.5) ^ (2*x) ≥ (0.5) ^ 1.5
Т.к. 0,5 < 1, то имеем:
2 * х ≤ 1.5
x ≤ 1.5 / 2
x ≤ 0.75 или иначе записать можно так х ≤ 
№ 5. 7 ^ (x ^ 2) * 49 ^ ( - x) ≥ 343
7 ^ (x ^ 2) * 7^2^ ( - x) ≥ 7 ^ 3
7 ^ (x ^ 2) * 7^ ( - 2 * x) ≥ 7 ^ 3
7 ^ ((x ^ 2) + ( - 2 * x)) ≥ 7 ^ 3
7 ^ (x ^ 2 - 2 * x) ≥ 7 ^ 3
Т.к. 7 > 1, то запишем так:
x ^ 2 - 2 * x ≥ 3
Решим получившееся квадратное неравенство.
x ^ 2 - 2 * x = 3
x ^ 2 - 2 * x - 3 = 0
D = 16
x1,2 = (2±4)/2
x1 = 3 и x2 = -1
Решим методом интервалов.
( - ∞; - 1 ] ∪ [ 3; + ∞ )
Y = 0.5*X² + 4X+10
1) Область определения - R - все по Х.
2) Находим ДИСКРИМИНАНТ квадратного уравнения и видим, что D= - 4
Вывод действительных корней - точек пересечения с осью Х - НЕТ
3) Для поиска экстремума находим производную
Y' = X+4. Минимум при Х= - 4 равен Y=2
4) Строим график для проверки
И - всё готово.