ответ: 2 игрок
Пошаговое объяснение: заметим, что в начале игры у числа остаток от деления на 3 равен двум. Тогда посчитаем кол-во в этом числе цифр с остатком 1 (9), 2(8) и 0(8). Тогда заметим, что выигрышной стратегией будет являться симметрия, те при ходе соперника мы будем делать так, чтобы остаток стал равен 2 снова (на 1 отвечаем 2, на 0 отвечаем 0, а 2 не может быть тк число станет кратно 3). Тогда заметим, что после хода по нашей стратегии у игрока во 1 останется хотя бы одна цифра (иначе остаток был бы равен 0), а во 2 число не будет кратно 3. Также заметим, что 2 игрок выигрывает при использовании данной стратегии, тк после его хода кол-во цифр всегда нечетно, поэтому когда-то после его хода останется одна цифра и ее удали 1 игрок, тем самым проигрывая. также заметим, что нам всегда будет хватать цифр для выполнения хода, тк если мы действовали симметрично и у оппонента хватило цифр для хода, то у нас тоже хватит
1. Область определения х∈(-∞;+∞)
2. Множество значений у∈[3;+∞)
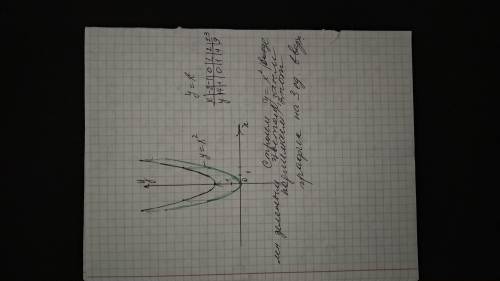
3. нулей нет. т.к. парабола у= х²поднята на 3 ед. вверх. ветви ее направлены вверх.
при любых значениях х у больше нуля.
4. функция возрастает при х∈[0;+∞) и убывает при х∈(-∞;0)
5. функция четна. т.к. ее график симметричен относительно оси оу.
6. ограничена снизу.
7. нет . не обратима. х²=у-3; х=±√(у-3), у=±√(х-3); но если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой, а вообще обратимая - это функция, у которой произвольному ее значению соответствует единственное значение аргумента.
график во вложении
1) Область определения?
2) Множество значений?
3) нули функции?
4) На каких интервалах функция убывает и возрастает?
5) Функция четная или нет?
6) Ограничена?
7) Обратима или нет?
Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными.
Четырехугольники бывают выпуклые (как ABCD) и
невыпуклые (A1B1C1D1).
Виды четырёхугольников
Параллелограмм
Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограммаСвойства параллелограмма
* противолежащие стороны равны;
* противоположные углы равны;
* диагонали точкой пересечения делятся пополам;
* сумма углов, прилежащих к одной стороне, равна 180°;
* сумма квадратов диагоналей равна сумме квадратов всех сторон:
d12+d22=2(a2+b2).
Признаки параллелограмма
Четырехугольник является параллелограммом, если:
1. Две его противоположные стороны равны и параллельны.
2. Противоположные стороны попарно равны.
3. Противоположные углы попарно равны.
4. Диагонали точкой пересечения делятся пополам.
Трапеция
Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Трапеция
Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.
Трапеция называется равнобедренной (или равнобокой) , если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Свойства трапеции
* ее средняя линия параллельна основаниям и равна их полусумме;
* если трапеция равнобокая, то ее диагонали равны и углы при основании равны;
* если трапеция равнобокая, то около нее можно описать окружность;
* если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
Признаки трапеции
Четырехугольник является трапецией, если его параллельные стороны не равны
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольникаСвойства прямоугольника
* все свойства параллелограмма;
* диагонали равны.
Признаки прямоугольника
Параллелограмм является прямоугольником, если:
1. Один из его углов прямой.
2. Его диагонали равны.
Ромб
Ромбом называется параллелограмм, у которого все стороны равны.
Свойства ромбаСвойства ромба
* все свойства параллелограмма;
* диагонали перпендикулярны;
* диагонали являются биссектрисами его углов.
Признаки ромба
1. Параллелограмм является ромбом, если:
2. Две его смежные стороны равны.
3. Его диагонали перпендикулярны.
4. Одна из диагоналей является биссектрисой его угла.
Квадрат
Квадратом называется прямоугольник, у которого все стороны равны.
Свойства квадратаСвойства квадрата
* все углы квадрата прямые;
* диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Признаки квадрата
Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.