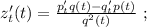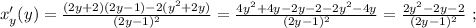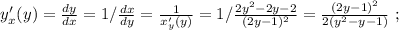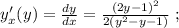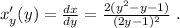
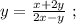
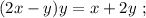
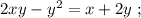
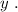Выражая из него 
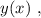мы получили бы стандартное выражение в виде корней параметрического квадратного уравнения, которых за исключением одной точки всегда 2, в том случае, если они конечно вообще есть. Таким образом, если бы мы использовали функцию 
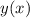относительно 
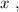для отображения того же множества точек, что и исходное уравнение, то такая функция, во-первых, не была бы однозначной, а во-вторых была бы определана не для всех 
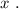Вывод: для дифференцирования такого уравнения наиболее удобно использовать именно однозначную обратную функцию 
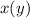относительно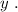 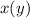относительно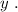 
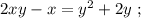
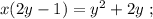
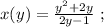
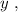используя общее правило,
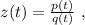то: 
