ДАНО: Y(x) = -x⁴ +2*x² + 1.
ИССЛЕДОВАНИЕ:
Описание ГЛАЗАМИ: Функция четвертого порядка с отрицательным коэффициентом - примерно парабола и ветви вниз. Должно быть четыре корня.
1. Область определения. Непрерывная. Разрывов нет.
D(x) = R = (-∞;+∞)
2. Корни функции: х₁ = - 1,55 и х₃ = 1,55.
Двух других нет. Нахождение самих корней - без комментариев.
3. Интервалы знакопостоянства (дополнительно к таблице).
Отрицательна: Y<0 X∈(-∞;-1.5)∪(1.55;+∞) - вне корней.
Положительна: Y>0 X∈(-1.55; 1.55) - между корнями.
4. Поиск экстремумов по первой производная функции .
Y'(x) = -4*х³ + 4*ч = 4*x*(1-x²) = 0
Точки экстремумов: x₅ = - 1, x₆ = 0, x₇ = 1
5 Локальные экстремумы:
Ymin(0) = 1 , Ymax(-1) = У(1) = 2
6. Интервалы монотонности.
Возрастает: Х∈(-∞;-1)∪(0;1) убывает: Х∈(-1;0)∪(1;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = -12*x² +4 = 0
x₈ = - √3/3 и х₉ = √3/3 - точки перегиба.
8. Выпуклая - "горка" - Х∈(-∞;-√3/3)∪(√3/3;+∞) .
Вогнутая - "ложка" - Х∈(-√3/3);(√3/3)
График на рисунке в приложении.
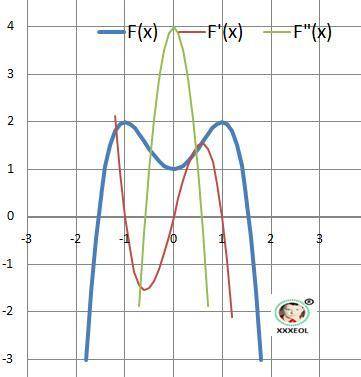
В точке D.
Пошаговое объяснение:
Пусть v1 - скорость первого пловца, v2 - скорость второго пловца, L - длина дорожки. Представим дорожку в виде отрезка с левой координатой 0 и с правой координатой L.
Пусть изначально пловцы находятся в точке C. После этого первый пловец двигается к 0, а потом к точке D. Второй пловец двигается к точке L, потом к точке D. На это тратится одинаковое время. То есть:
v1*(C-0+D-0) = v2*(L-C+L-D)
Отсюда v1/v2 + 1 = 2L/(C+D).
Аналогично, пусть они стартуют из точки D, а заканчивают путь в точке E. Тогда получается выражение v1*(D-0+E-0) = v2*(L-D+L-E).
Из него получается v1/v2 + 1 = 2L/(D+E).
Таким образом, v1/v2 + 1 = 2L/(C+D) = 2L/(D+E), то есть E = C.
Такое же действие можно проделать и при движении из точки E в точку F. Получится, что v1/v2 + 1 = 2L/(E+F). Вместо E подставим C, а потом соединим это равенство с равенством v1/v2 + 1 = 2L/(C+D). Получится, что F = D.
Далее очевидно, что точки C и D будут чередоваться, а 20-я встреча произойдет в точке D.
16*7=121
Возможно так)