128√3 (м²)
Пошаговое объяснение:
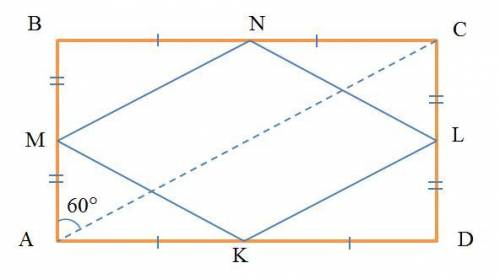
Перевод: Меньшая сторона прямоугольника равна 16 м и образует с его диагональю угол 60°. Середины всех сторон прямоугольника последовательно соединены. Найдите площадь образованного четырехугольника.
Решение.
По определению тангенса угла BAC (см. рисунок):
tg∠BAC= BC/AB.
Отсюда, учитывая AB=16 м и ∠BAC = 60°, получим
BC = AB•tg60° = 16√3 м.
Соединяем середины M, N, L и K прямоугольника. Так как MK=MN=LN=LK как гипотенузы равных треугольников, то получаем ромб, диагонали которого равны
KN = AB = 16 м, ML = BC = 16√3 м.
Определим площадь ромба через его диагонали:
S = (d1·d2)/2 = (ML·KN)/2 = (16 · 16√3)/2 = 128√3 (м²).
б) x=0
в) x=37/3,7
x=10
г) x^2=x
x^2-x=0
x(x-1)=0
x=0
x=1
д) a^3-a=0
a(a^2-1)=0
a=0
a=+-1
е) m^3-m^2=0
m^2(m-1)=0
m=0
m=1