a=-6
Пошаговое объяснение:
(|x|-2)(|x|-4)=2-a
(|x|-2)(|x|-4)-2+a=0
рассмотрим функцию f(x)=(|x|-2)(|x|-4)-2+a
Она непрерывна на всей числовой оси.
f(-x)=(|-x|-2)(|-x|-4)-2+a=(|x|-2)(|x|-4)-2+a=f(x) ⇒ функция четная.
Если четная функция имеет НЕчетное количество корней, то один из них обязательно будет 0.
для уравнения: (|x|-2)(|x|-4)=2-a, при х=0, получаем
(0-2)(0-4)=2-a
-2*(-4)=2-a
8=2-a
a=2-8
a=-6 - при таком значении a уравнение имеет нечетное число различных корней.
Проверим, будет ли их ровно 3:
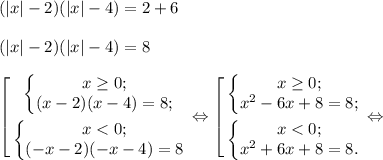
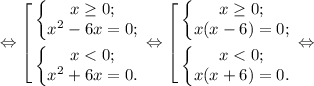
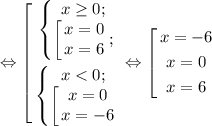
Действительно, при a=-6 получилось 3 корня!
ответ: a=-6
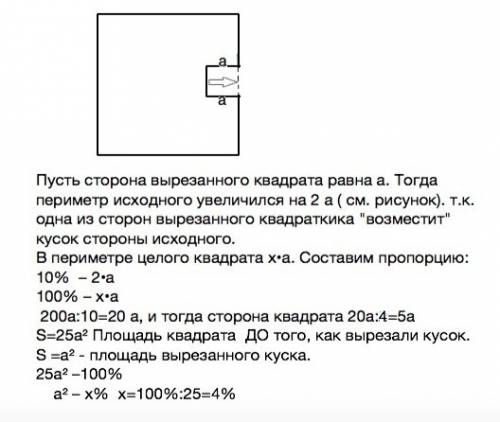
Пусть сторона вырезанного квадрата равна а.
Тогда периметр исходного увеличился на 2 а ( см. рисунок). т.к. одна из сторон вырезанного квадратика "возместит" кусок стороны исходного.
В периметре целого квадрата х•а. Составим пропорцию:
[ 10% – 2•а
[100% – х•а
х=200а:10=20 а, и тогда сторона квадрата 20а:4=5а
S=25a² – площадь квадрата ДО того, как вырезали кусок.
S =a² - площадь вырезанного куска.
[ 25а² –100%
[ а² – х% ⇒ х=100%:25=4%
На 4% уменьшилась площадь исходного квадрата
так ка 728:8=91 а тут 104