log(1 + 1/(x + 1)²) (x² + 3x + 2)/(x² - 3x + 4) ≤ 0
одз
1 + 1/(x + 1)² > 0 x ∈ R
1 + 1/(x + 1)² ≠ 1 x ∈ R
(x + 1) ≠ 0 x ≠ -1
(x² + 3x + 2)/(x² - 3x + 4) > 0
x² + 3x + 2 = 0 D = 9 - 8 = 1 x12 = (-3 +- 1)/2 = -2 -1
x² - 3x + 4 = 0 D = 9 - 16 < 0 x∈ R
(x + 1)(x + 2) > 0
x∈ (-∞, -2) U (-1, +∞)
log(1 + 1/(x + 1)²) (x² + 3x + 2)/(x² - 3x + 4) ≤ log(1 + 1/(x + 1)²) 1
1 + 1/(x + 1)² > 1 всегда
(x² + 3x + 2)/(x² - 3x + 4) ≤ 1
(x² + 3x + 2)/(x² - 3x + 4) - 1 ≤ 0
(x² + 3x + 2 - (x² - 3x + 4)) ≤ 0
знаменатель отбрасываем (x² - 3x + 4) он всегда >0
(x² + 3x + 2 - x² + 3x - 4) ≤ 0
6x - 2 ≤ 0
x ≤ 1/3
x∈ (-∞, -2) U (-1, 1/3]
ОДЗ:
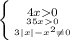 ⇒
⇒ 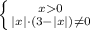 ⇒ x ∈(0;3) U (3:+∞)
⇒ x ∈(0;3) U (3:+∞)
на ОДЗ
|x|=x
Неравенство можно записать так:
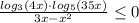
Метод интервалов
нули числителя:
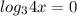 или
или 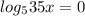
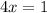 или
или 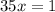
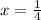 или
или 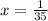
нули знаменателя:
x=0; x=3
Так как
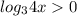 при
при 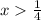 а
а 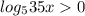 при
при 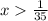
Поэтому на 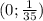 и на
и на 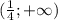 числитель положителен, на
числитель положителен, на 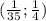 отрицателен.
отрицателен.
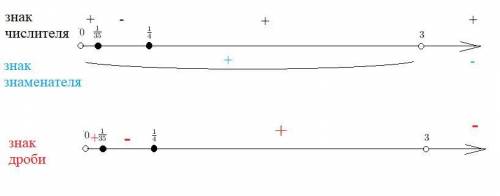
Знаменатель положителен на (0;3) и отрицателен на (3;+∞)
Знаки дроби ( cм рис.)
О т в е т. ![[\frac{1}{35}; \frac{1}{4}] \cup (3;+\infty)](/tpl/images/1358/6903/5686b.png)
Дробь неположительна, если числитель и знаменатель разных знаков.
Можно рассмотреть две системы неравенств.
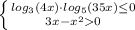 или
или 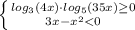
a = 3.5 м - длина, b = 3 м - ширина, c = 2,4 м - высота.
2) вычисляем объем комнаты по формуле
V = a*b*c = 3.5 м * 3 м *2.4 м = 25.2 м³
3) Вычисляем объем кислорода в воздухе комнаты.
Vкисл = 23,1 м³ * 0,21 = 5,292 м³ ~ 5.3 м³
ОТВЕТ: Кислорода примерно 5,3 м³.