ответ:
чтобы решить заданные примеры, сначала необходимо выполнить действия в скобках, а потом за скобками, сначала выполняем умножение и деление, а после этого прибавление и отнимание:
1. (2928 - 88) : 142 = 20.
1) 2928 - 88 = 2840;
2) 2840 : 142 = 20.
2. (64 + 37) * 91 = 101 * 91 = 9191.
3. 1032 : (5472 : 19 : 12) = 43.
1) 5472 : 19 = 288;
2) 288 : 12 = 24;
3) 1032 : 24 = 43.
4. 15732 : 57 : (156 : 13) = 23.
1) 156 : 13 = 12;
2) 15732 : 57 = 276;
3) 276 : 12 = 23.
5. (880 + 230) * 54 : 37 = 1110 * 54 : 37 = 59940 : 37 = 1620.
6. (3211 + 103 * 23) : 124 = (3211 + 2369) : 124 = 5580 : 124 = 45.
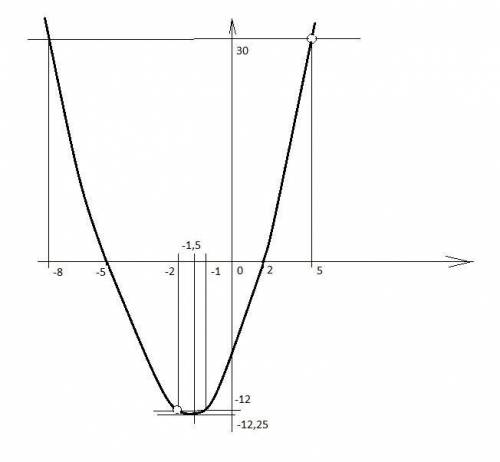
-12,25;-12;30
Пошаговое объяснение:

А вот дальше тонкий момент. Если бы нас просили упростить, то можно было бы сократить скобки (x+2)(x-5), и осталось бы квадратное выражение.
Но у нас функция, в которой изначально эти две скобки стоят в знаменателе. Значит, по области определения, x ≠ -2 и x ≠ 5.
Это так называемые устранимые разрывы.
То есть графиком будет парабола y = x^2 + 3x - 10 с двумя выколотыми точками: x = -2; y = (-2)^2 + 3(-2) - 10 = -12 и x = 5; y = 5^2 + 3*5 - 10 = 30.
Значит, по 1 точке пересечения будут иметь прямые y = -12 и y = 30.
Они пересекаются с графиком в точках
x = -1; y = (-1)^2 + 3(-1) - 10 = -12 и x = -8; y = (-8)^2 + 3(-8) - 10 = 30.
Кроме того, у параболы еще есть вершина:
x0 = -b/(2a) = -3/2 = -1,5; y0 = (-1,5)^2 + 3(-1,5) - 10 = -12,25.
Значит, прямая y = -12,25 тоже имеет 1 точку пересечения с графиком.
Примерный график я нарисовал, но вы в тетради по клеточкам нарисуете лучше.