Понятия множеств, их пересечений и соответствий изучаются как основы программирования и алгоритмики в ССУЗах и ВУЗах. Для дошкольников такие задания немыслимы, т.к. мозг дошкольника еще не готов вопринимать такую сложную информацию.
Все же простой пример сопоставления множеств для дошкольника приведу:
Дано: 2 круга (множества)
1 круг: нарисованы девочки и мальчики в шарфиках и шапочках разных цветов (желательно, простой спектр: синий, желтый, красный, зеленый)
2 круг: варежки аналогичных цветов
Задание: сопоставить каждому ребенку в шарфике и шапочке варежки
Пошаговое объяснение:
Пошаговое объяснение:
Пусть скорость третьего велосипедиста равна v км/ч, а t ч— момент времени, когда он догнал второго велосипедиста. Начало отсчёта времени — момент, когда первый велосипедист начал движение. Тогда к моменту времени t, когда третий велосипедист догонит второго, второй велосипедист проедет расстояние 16(t-1) км, а третий — расстояние v(t-2) км.Аналогично: к моменту времени t+4 когда третий велосипедист догонит первого, первый велосипедист проедет 18 (t+4) км, а третий, поскольку он был в пути на два часа меньше, проедет v(t+2) км. Составим систему уравнений:
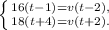
Умножим первое уравнение на t+2 а второе — на t-2 и вычтем первое уравнение из второго.
-6x=-8
x=8:6
x=1 1/3
2)
2/3x=-3/8
x=-3/8*3/2
x=-9/16
3)
40,5:x=-9
x=40,5:(-9)
x=-4,5
4)
-32/63:x=8/21
x=-32/63*21/8
x=-4/3
x=-1 1/3
5)
x:2/7=-1,4
x=-1,4*2/7
x=-14/10*2/7
x=-2/5
x=-0,4