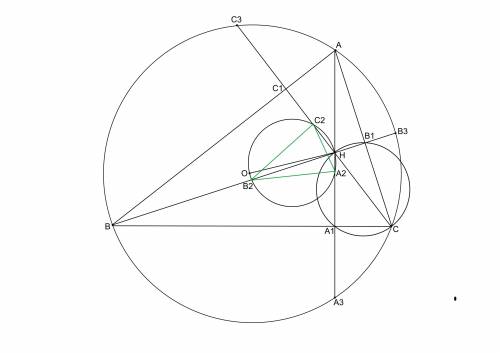
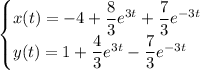1) Все середины хорд, проходящих через точку внутри окружности (пусть это точка H, пока не важно, что это ортоцентр ΔABC) лежат на окружности, построенной на отрезке OH, как на диаметре. См. чертеж, О - центр большой окружности.
Например, хорда СС3, середина С2, угол OC2H прямой, так как диаметр, который делит хорду пополам, перпендикулярен ей. Поэтому С2 лежит на указанной окружности. Это справедливо для любой хорды, проходящей через точку H
2) Таким образом, если соединить середины хорд AA3, BB3 и CC3, то получится ΔA2B2C2, вписанный в окружность, построенную на отрезке ОН, как на диаметре. Разумеется, на этой окружности лежат и точки O и H.
3) Поскольку в этой задаче точка H - ортоцентр ΔABC, очень легко установить соответствие между углами ΔABC и ΔA2B2C2.
Проще всего увидеть, что ∠A2B2C2 =∠ABC, так как оба составляют 180° в сумме с ∠C1HA1.
В самом деле, четырехугольник B2C2HA2 вписанный, поэтому ∠A2B2C2 + ∠C1HA1 = 180°,
В четырехугольнике BC1HA1 два угла прямые, поэтому сумма двух других углов тоже 180°
∠ABC + ∠C1HA1=180°,
Поэтому ∠ABC = ∠A2B2C2;
4) ∠B2C2A2 = ∠B2HA2 оба угла вписаные и опираются на одну и ту же дугу. Поэтому ∠B2C2A2 = 180° - ∠B1HA1 = ∠BCA; последнее равенство справедливо по такой же причине, что и в пункте 3) - в четырехугольнике BC1HA1 два угла прямые, поэтому сумма двух других углов тоже 180°.
Поскольку два угла ΔABC и ΔA2B2C2 равные, эти треугольники подобны, чтд
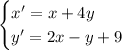
Преобразования Лапласа:
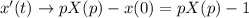
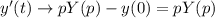
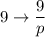
Получаем систему, для краткости записав 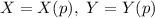 :
:
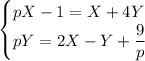
Из второго уравнения выразим Y:
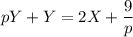
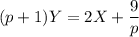
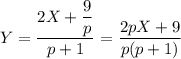
Подставим в первое уравнение и выразим Х:
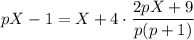
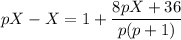
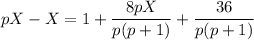
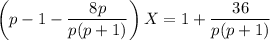
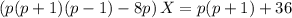
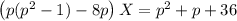
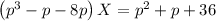
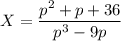
Выражаем Y:
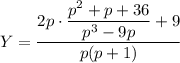
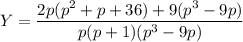
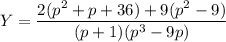
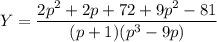
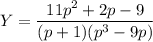
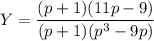
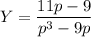
Разложим дроби, соответствующие Х и Y, на составляющие:
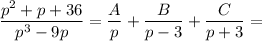
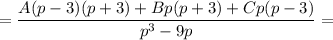
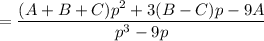
Получаем условие равенства:
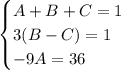
Из третьего уравнения:
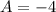
Остается два уравнения:
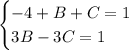
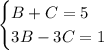
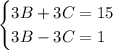
Сложим уравнения:
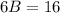
Находим В:
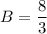
Находим С:
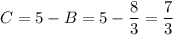
Итак, представление для Х:
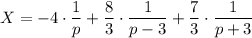
Преобразуем Y:
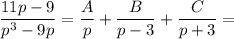
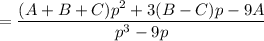
Получаем условие равенства:
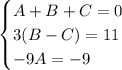
Из третьего уравнения:
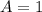
Остается система:
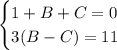
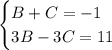
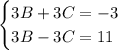
Сложим уравнения:
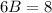
Находим В:
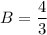
Находим С:
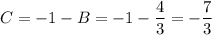
Представление для Y:
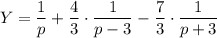
Решение, записанное в изображениях:

Обратное преобразование Лапласа:
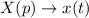
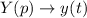
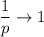
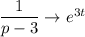
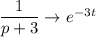
Искомое решение: