Для всех равных пар натуральных чисел
Пошаговое объяснение:
Пусть канонические виды чисел x и y таковы:
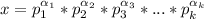
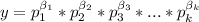
где 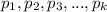 - простые числа, а
- простые числа, а
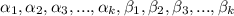 - целые неотрицательные степени простых чисел (некоторые могут равняться нулю).
- целые неотрицательные степени простых чисел (некоторые могут равняться нулю).
Тогда по свойству НОД(x; y)=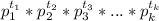
где 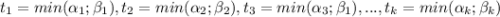
По условию НОД(x; y)²=x · y и отсюда следует, что
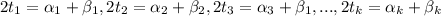
Очевидно, что значение min(m; n) или m или n. Поэтому, если
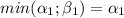 , то из равенства
, то из равенства 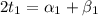 следует, что
следует, что 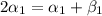 и
и 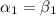 . Точно такое равенство можно установить если
. Точно такое равенство можно установить если 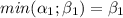 .
.
И такие равенства получаются для других степеней простых чисел.
Отсюда заключаем, что НОД(x; y)²=x · y, тогда и только тогда, когда x=y.
Отсюда следует ответ к задаче: для всех равных пар натуральных чисел.
первое число – количество спичек.
Последующие числа: ходы игроков, в квадратных скобках [] – указаны ходы соперника
1 1 – выигрыш
2 2 – выигрыш
3 нет выигрышной стратегии
4 1, [1 или 2], 2 или 1 – выигрыш
5 5 – выигрыш
6 1 – гарантирует выигрыш соперника (см. пункт 5 с инверсией позиций).
6 2 – гарантирует выигрыш соперника (см. пункт 4 с инверсией позиций).
6 5 – гарантирует выигрыш соперника (см. пункт 1 с инверсией позиций).
6 нет выигрышной стратегии
7 1, далее у соперника нет шансов (см. пункт 6 с инверсией позиций).
8 2, далее у соперника нет шансов (см. пункт 6 с инверсией позиций).
9 1 – гарантирует выигрыш соперника (см. пункт 8 с инверсией позиций).
9 2 – гарантирует выигрыш соперника (см. пункт 7 с инверсией позиций).
9 5 – гарантирует выигрыш соперника (см. пункт 4 с инверсией позиций).
9 нет выигрышной стратегии
10 1, далее у соперника нет шансов (см. пункт 9 с инверсией позиций).
11 2, далее у соперника нет шансов (см. пункт 9 с инверсией позиций).
12 1 – гарантирует выигрыш соперника (см. пункт 11 с инверсией).
12 2 – гарантирует выигрыш соперника (см. пункт 10 с инверсией).
12 5 – гарантирует выигрыш соперника (см. пункт 7 с инверсией).
12 нет выигрышной стратегии
Просматривается индукционный вывод.
Допустим, мы знаем, что:
3n–2 выигрыш гарантирован
3n–1 выигрыш гарантирован
3n нет выигрышной стратегии
3n+1 выигрыш гарантирован
3n+2 выигрыш гарантирован
Это верно для n = 3.
Тогда:
3n+3 1 – гарантирует выигрыш соперника (см. пункт 3n+2 с инверсией).
3n+3 2 – гарантирует выигрыш соперника (см. пункт 3n+1 с инверсией).
3n+3 5 – гарантирует выигрыш соперника (см. пункт 3n–2 с инверсией).
3(n+1) нет выигрышной стратегии
3(n+1)+1 1, далее у соперника нет шансов (см. пункт 3(n+1) с инверсией).
3(n+1)+2 2, далее у соперника нет шансов (см. пункт 3(n+1) с инверсией).
Значит всё сказанное в допущении верно и для n+1,
т.е. для n=4, n=5, n=6, n=7 и т.д.
О т в е т :
Первый может гарантированно выиграть, если число спичек на столе не кратно трём. Стало быть, ему нужно всегда оставлять на столе перед соперником число спичек кратное трём. Если в очередном ходе начавшего игру на столе лежит число спичек больше кратного трём на единицу (1, 4, 7, 10, 13 и т.п.), то начавший игру должен брать одну спичку, оставляя сопернику кратное трём. Если в очередном ходе начавшего игру на столе лежит число спичек больше кратного трём на двойку (2, 5, 8, 11, 14 и т.п.), то начавший игру должен брать две или пять спичек (если это возможно), оставляя сопернику кратное трём.
Второй может гарантированно выиграть, если начальное число спичек на столе кратно трём. В любом ходе ему нужно всегда оставлять на столе перед начавшим игру число спичек кратное трём. Если в очередном ходе второго игрока на столе лежит число спичек больше кратного трём на единицу (1, 4, 7, 10, 13 и т.п.), то второй игрок должен брать одну спичку, оставляя начавшему – кратное трём. Если в очередном ходе второго игрока на столе лежит число спичек больше кратного трём на двойку (2, 5, 8, 11, 14 и т.п.), то второй игрок должен брать две или пять спичек (если это возможно), оставляя начавшему – кратное трём.
.