Найдите расстояние между точками a(-2,7) и b(2,4)

Question

Математика: Найдите расстояние между точками a(-2,7) и b(2,4)

RedBalloon · Accepted Answer

Опускаем высоту пирамиды (т.к. все грани наклонены под одним углом к плоскости основания, то она упадёт в центр треугольника О). Основание - правильный треугольник со стороной 12, поэтому медина АН (которая совпадает с высотой и поэтому просчитывается через теорему Пифагора) равна 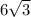$6\sqrt3$ . Основанием высоты пирамиды О АН делится в отношении 2:1 (центр правильного треугольника), поэтому ОН= 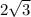$2\sqrt3$ . Если вершина пирамиды S, то SO лежит в прямоугольном треугольнике SOH против угла в 60 градусов, а ОН= 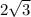$2\sqrt3$ , т.е. tg60=SO/OH, SO=OH*tg60= 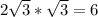$2\sqrt3*\sqrt3=6$ . Площадь основания равна 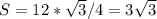$S=12*\sqrt3/4=3\sqrt3$ (площадь правильного треугольника). Объём равен

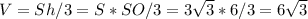
$V=Sh/3=S*SO/3=3\sqrt3*6/3=6\sqrt3$

MOGZ ответил