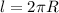 длина окружности
длина окружности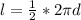
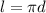
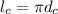 длина экватора Сатурна
длина экватора Сатурна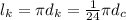 длина экватора Каллисто
длина экватора Каллисто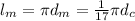 длина экватора Марса
длина экватора Марса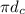 одинаково, значит можно рассматривать только коэффициенты
одинаково, значит можно рассматривать только коэффициенты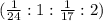
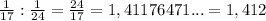
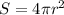 - площадь поверхности шара
- площадь поверхности шара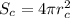 площадь поверхности Сатурна
площадь поверхности Сатурна площадь поверхности Каллисто
площадь поверхности Каллисто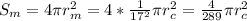 площадь поверхности Марса
площадь поверхности Марса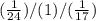
Если подставить п/12, то получим cosп/2 а это 0, значит все выражение = 0
2. = 2 × 1/√7х × (√7х)'=2 × 1/√7х × 1/2√7х × (7х)'=2 × 1/√7х × 1/2√7х × 7=1/х
Если подставить 1/5, то получим 5
3. =cos(4*x+x*3)×(4*x+x*3)'=cos(4*x+x*3)×(4*x × ㏑4x+3x²)