x ∈ (1; 2] ∪ {3}
Пошаговое объяснение:
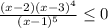
решим неравенство методом интервалов. Для этого приравняем и числитель и знаменатель к нулю:
x-2=0; x=2
x-3=0; x=3
x-1=0; x=1
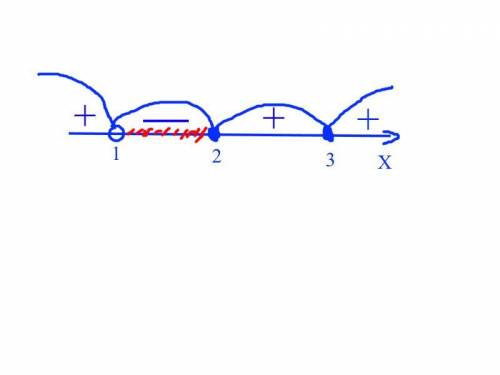
изобразим точки на координатной прямой. Точка "1" будет выколота, так как она обнулит знаменатель, а на 0 делить нельзя. Точки "2" и "3" будут закрашенными, т.к знак неравенства "меньше или равно" (см рис)
знак крайнего правого интервала будет + (можно взять число "100" и подставить в неравенство), дальше "+"; "-"; "+" (подставляем точки из этих интервалов в неравенство и ищем знак)
т.к знак неравенства "≤0", то выбираем интервалы с "-"
также отдельно берем точку "3", т.к она обнулит числитель, а это нас устраивает
x ∈ (1; 2] ∪ {3}
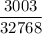
Пошаговое объяснение:
Пусть в каждом гардеробе было по 15 мест, представим гардероб как последовательность нулей и единиц: 0 — школьник разделся в другом гардеробе, 1 — школьник разделся в этом гардеробе. Тогда ситуация выглядит примерно так:
I: 110010100011101
II: 001101011100010
Если в первом гардеробе задана некоторая последовательность, то она однозначно задаёт последовательность второго гардероба. На каждой позиции первого гардероба может быть либо 0, либо 1, поэтому, учитывая однозначность, всего возможных ситуаций 2¹⁵ = 32768.
Если в правом гардеробе занято вдвое мест, чем в левом, то есть вдвое больше единиц, чем в левом (10 в правом, 5 в левом), то искомое количество подходящих ситуаций — число расставить 10 единиц в правом гардеробе.
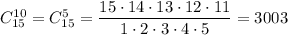
Искомая вероятность равна 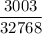 .
.
Равенство всех пяти сумм чисел, стоящих в вершинах треугольников, выражается уравнениями:
Заметим, что во всех суммах, помимо прочих (что можно легко понять и просто из рисунка) присутствует одно и то же число
Так что это число может быть совершенно произвольным: простым, натуральным, целым, дробным, иррациональным, да хоть комплексным... Это ничего не изменит, поскольку данное число входит во все суммы в единичном экземпляре.
Вычеркнем из вышеозначенных уравнений проанализированное число и рассмотрим уравнения в упрощённом варианте:
Из первого равенста следует, что:
Из третьего равенста следует, что:
Поскольку:
Из второго равенста следует, что:
Таким образом, все «вершинные» числа должны быть равны между собой, а центральное при этом может быть каким угодно.
Значит на рисунке может оказаться одно или два различных числа.
Максимум : 2 .
О т в е т : 2 .