12 лет.
Пошаговое объяснение:
Пусть сестре х лет, а мальчик в n раз старше её, тогда мальчику х•n лет, а дедушке (х•n)•n лет.
Зная, что мальчику и дедушке вместе 84 года, составим уравнение:
х•n + (х•n)•n = 84
х•n•(1 + n) = 84
Разложим 84 на простые множители:
84 = 2•2•3•7
Разложение, в котором три натуральных множителя, два из которых n и n + 1 являются последовательными натуральными числами, может выглядеть так:
84 = 1 • 2 • 42, 84 = 2 • 3 • 14 или 84 = 2 • 6 • 7.
х•n•(1 + n) = 42 • 1 • 2 - не удовлетворяет условию, т.к. х < 7..
х•n•(1 + n) = 14 • 2 • 3 - не удовлетворяет условию, т.к. х < 7..
х•n•(1 + n) = 2 • 6 • 7 - удовлетворяет условию, х = 2, 2 < 7.
Сестре сейчас 2 года, мальчику - 2 • 6 = 12 (лет), дедушке - 12•6 = 72 (года).
12 + 72 = 84 (года) - верно
0.8
Пошаговое объяснение:
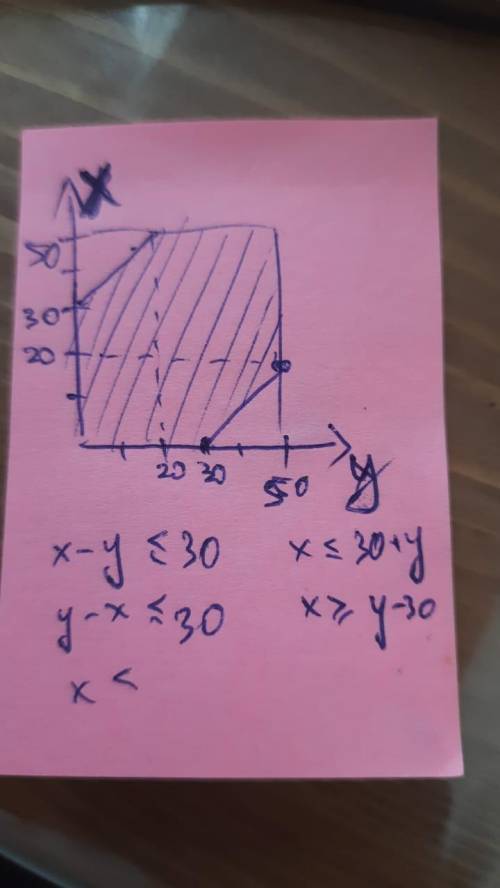
Задача эквивалентна той, что в промежутке времени с 12:20 до 13:10 берется две случайные точки (длина промежутка = 50 минут), и нужно найти вероятность того, что расстояние между точками будет не более 30 минут (точки = моменты прихода товарищей). На первом фото изображено множество возможных пар x и y - это квадрат 50 на 50 - это множество возможных исходов (площадь этой области 50*50=2500). Благоприятные из них - это те, для которых расстояние между x и y не больше 30 минут. то есть x-y≤30 и y-x≤30 заштриховал эту область на рисунке.
На втором рисунке считаю площадь "благоприятной области":
400+100+400+200+900=2000
А вероятность того, что пара (x;y) из квадрата 50 на 50 попадет в благоприятную область тогда будет равна 2000/2500=20/25=4/5=0.8

вот так вот