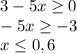
Пошаговое объяснение:
нам задан эллипс с полуосями 1 и 2
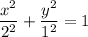
тогда мы можем посчитать площадь фигуры двумя
1
теперь считаем площадь фигуры заданной параметрически
формула для вычисления
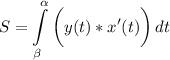
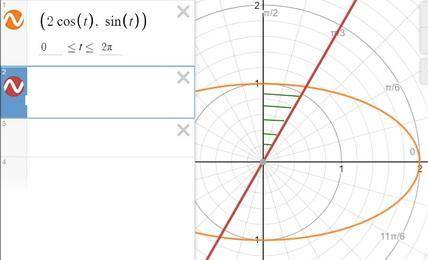
здесь заметим, что параметрические уравнения «прорисовывают» дугу эллипса «в противоход» оси х , а площадь фигуры считается слева направо. поэтому нижнему пределу интегрирования соответствует значение π/2, а верхнему пределу – значение π/3
тогда мы будем иметь
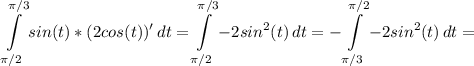
![\displaystyle = 2\int\limits^{\pi/2}_{\pi/3} {\bigg (\frac{1}{2} -\frac{1}{2} cos(2t)\bigg )} \, dt=t\bigg |_{\pi/3}^{\pi/2}-\int\limits^{\pi/2}_{\pi/3} {cos(2t)} \, dt =\frac{\pi}{6} -\left[\begin{array}{ccc}u=2t \quad du=2dt\\u_1=\displaystyle \frac{2\pi}{3} \quad u_2=\pi\\\end{array}\right] =](/tpl/images/2008/1017/b5d5c.png)
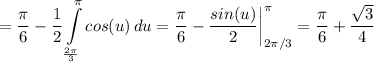
2
считаем в декартовых координатах
это будет криволинейная трапеция, прилегающая к оси ОУ
формула
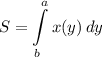
найдем х(у)
тогда считаем площадь
![\displaystyle S= \int\limits^1_0 {\frac{\sqrt{4-y^2} }{2} } \, dy=\left[\begin{array}{ccc}y=2sin(u)\hfill\\dy=2cos(u)du\hfill\\u_1=0\quad u_2=\pi/6\end{array}\right] =\int\limits^{\pi/6}_0 {2cos^2(u)} \, du](/tpl/images/2008/1017/b1bd7.png)
здесь заменяем
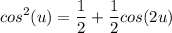
и дальше уже по накатанной схеме (как в первом случае)
в результате получим тот же ответ
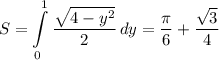(кто не верит может пересчитать -)) )
графики прилагаются
1 в полярных координатах
2 в декартовых координатах
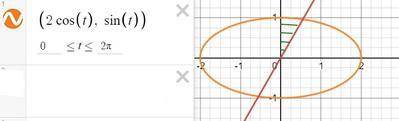
Т=1, О=4, Р=7.
ТОРТ = 1471.
Пошаговое объяснение:
ТОРТ+ОРТ+РТ+Т=2014
ТОРТ = Т•1000 + О•100 + Р•10 + Т;
ОРТ = О•100 + Р•10 + Т;
РТ = Р•10 + Т, тогда
1000Т + 100О + 10Р + Т + 100О + 10Р + Т + 10Р + Т + Т = 2014
Упростим левую часть равенства:
1004Т + 200О + 30Р = 2014
1) Если Т = 2, то
2008 + 200О + 30Р = 2014
Не существует таких цифр О и Р, при которых 200О + 30Р = 6.
2) Т = 1, других вариантов нет, тогда
1004 + 200О + 30Р = 2014
200О + 30Р = 2014 - 1004
200О + 30Р = 1010
О меньше, чем 5.
1) Если О = 4, то
800 + 30Р = 1010
30Р = 1010 - 800
30Р = 210
Р = 210:30
Р = 7
Первый вариант:
Т=1, О=4, Р=7.
2) Если О = 3, то
600 + 30Р = 1010
30Р = 1010 - 600
30Р = 410
410 не делится нацело на 30, такой вариант невозможен. Этот и последующие варианты невозможны и потому, что Р > 10, что невозможно для цифры.
