Відповідь:
Мотоциклист был в пути 40 минут или 2/3 часа ( 0,67 часа ).
Покрокове пояснення:
В 8-00 вышел пешеход, в 10-00 выехали мотоциклист и велосипедист. В 10-15 мотоциклист обогнал пешехода, а в 11-00 велосипедист обогнал пешехода.
До момента встречи пешехода и мотоциклиста пешеход был в дороге 2,25 часа, а мотоциклист - 0,25 часа. Следовательно скорость мотоциклиста в 2,25 / 0,25 = 9 раз больше скорости пешехода.
До момента встречи пешехода и велосипедиста пешеход был в дороге 3 часа, а велосипедист - 1 час. Значит скорость велосипедиста в 3 / 1 = 3 раза больше скорости пешехода.
Пешеход был в пути 14 - 8 = 6 часов.
Мотоциклист был в пути 6 / 9 = 2/3 часа = 40 минут ( прибыл в пункт Б в 10-40 ).
Велосипедист был в пути 6 / 3 = 2 часа ( прибыл в пункт Б в 12-00 ).
(см. объяснение)
Пошаговое объяснение:
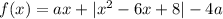
Заметим, что функция непрерывна и на бесконечностях стремится к плюс бесконечности. Тогда она имеет свой минимум при любом значении параметра.
Выполним наложение условия:
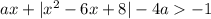
Нам надо найти такие значения параметра, чтобы это неравенство было истинно при любом значении переменной  .
.
Откуда перейдем к более удобному виду:

Слева нет параметра. Тогда эту чисть неравенства построим в координатах (x; y), понимая, что она будет фиксирована.
Справа находится параметрическая прямая, вращающаяся вокруг точки (4; 0). Ее тоже строим в той же системе координат.
Тогда задача заключается в том, чтобы сделать так, когда вся левая часть неравенства находится выше прямой.
Покажем соответствующие расположения прямой:
(см. прикрепленный файл)
В первом случае, она касается параболы 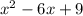 .
.
Тогда:

Здесь  постороннее значение.
постороннее значение.
Во втором случае, прямая проходит через точку (2; 1).
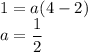
Итого при 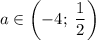 наименьшее значение функции больше минус одного.
наименьшее значение функции больше минус одного.
Задание выполнено!
