а) 1/36
б) 7/8
Пошаговое объяснение:
а) При бросании первой игральной кости общее количество исходов равно 6. Только при одном исходе выпадет число 5. Значит вероятность такого события равна 1/6.
При бросании второй игральной кости общее количество исходов равно 6. При двух исходах выпадет число большее, чем 4 (т.е. 5 и 6). Значит вероятность такого события равна 2/6=1/3.
При бросании третьей игральной кости общее количество исходов равно 6. При трех исходах выпадет нечетное количество очков (т.е. 1, 3 и 5). Значит вероятность такого события равна 3/6=1/2.
Осталось перемножить полученные вероятности.
Получим 1/6 * 1/3 * 1/2 = 1/36 - искомая вероятность события.
б) Бросают три игральные кости. Общее количество исходов n=6*6*6=216
Событие А - "хотя бы на одной кости выпало четное количество очков".
Противоположное ему событие ¬А - "ни на одной кости не выпало четное количество очков". m- число исходов, благоприятствующих наступлению события ¬A. m=3*3*3=27
Значит, вероятность Р(¬А)= m/n = 27/216 = 1/8
Искомая вероятность Р(А)= 1-Р(¬А) = 1-1/8 = 7/8
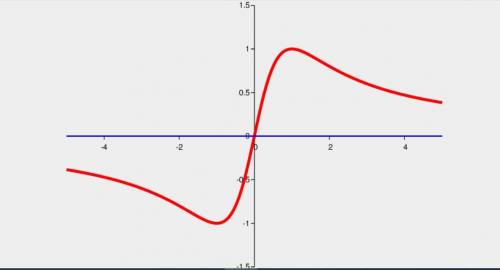
Дана функция y = 2x/(x² + 1.
Функция нечетная.
Условия для точек разрыва : x² + 1 = 0, x² = -1.
Точки разрыва : нет.
Корни функции (точки пересечения с осью абсцисс x) : x = 0.
Вычисление y′ : y′=2⋅1(x²+1)−x(2x)(x²+1)2=2⋅1−x²(x²+1)2=−2(x−1)(x+1)(x2+1)2
Первая производная : y′=−2(x−1)(x+1)/(x²+1)²
Условия для стационарных точек : −2(x−1)(x+1)=0
Стационарные точки : х1=−1, х2=1
Вторая производная : y′′=4x(x²−3)/(x²+1)³
Условия для критических точек : 4x(x²−3)=0
Критические точки : х1=−√3, х2=√3, х3=0
Асимптота на обоих ±∞ линия y=0.
ответ:2/5занята кабачками