(1 + 2) * 3 = 9;
1 * 2 * 3 + 4 = 10;
1 - 2 + 3 + 4 + 5 = 11;
тут терпение закончилось
(1 + (2 - 3) * (4 - 5)) * 6 = 12;
- 1 + (2 * (3 - 4) * (5 - 6)) * 7 = 13;
1 * 2 * (3 + 4) + (5 - 6) - (7 - 8) = 14;
(1 * 2 + (- 3 + 4)) * 5 + (-6 + 7) + (8 - 9) = 15;
Пошаговое объяснение:
Месяц или 2 назад скачал крякнутую NeuroNative, там такие же странные задачи были, но с постепенным усложнением.
Суть в том, что ты вспоминаешь как можно было бы получить число справа, к примеру, 9 -- это три умножить на три.
Потом, смотришь, есть ли в последовательности участник получения, условно, девятки. К примеру, в последовательности 1, 2, 3 есть тройка.
Потом, смотришь, можно ли из оставшихся цифр получить других участников получения, условно, девятки. К примеру, можно ли из 1 и 2 получить тройку?
Иногда, оставались числа, которые мне были не нужны, и так как каждое следующее число больше предыдущего на 1, то на их разницу, к примеру на (-5+6), можно умножить всё остальное и тогда результат не изменится! Кроме того, из пары соседних чисел можно получить не только 1, но и -1, а если сложить 1 и -1, то получится ноль, сложение с которым тоже никак не повлияет на результат!
Пошаговое объяснение:
Количество клеток на доске 8×8 равно 64. Если удалить 1 клетку останется 63 клеток. Поэтому условие означает, что на доску 8×8 уложена 21 прямоугольников 1×3 (или 3×1).
Нам нужно вырезать клетку из доски 8×8 так, чтобы остаток можно было покрыть прямоугольников 1×3 (или 3×1).
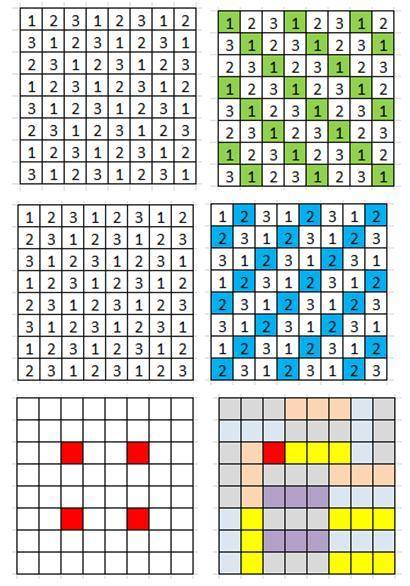
Раскрасим доску 8×8 в 3 цвета вдоль главной диагонали так, чтобы любой прямоугольник занимал по клетке каждого цвета (см. рисунок-1). Клеток с номерами 1 – 22 штуки, с номером 2 – 21 штуки, с номерами 3 – 21, таким образом, чтобы разрезать доску на прямоугольников 1×3 (или 3×1), можно отрезать одну клетку цвета – 1 (чтобы всех цветов осталось поровну). Такие клетки закрашены зелёным цветом (см. рисунок-2).
Раскрасим теперь доску в три цвета вдоль других диагоналей (см. рисунок-3). Клеток с номерами 1 – 21 штуки, с номером 2 – 22 штуки, с номерами 3 – 21, таким образом, чтобы разрезать доску на прямоугольников 1×3 (или 3×1), можно отрезать одну клетку цвета – 2 (чтобы всех цветов осталось поровну). Такие клетки закрашены голубым цветом (см. рисунок-4).
Таким образом, мы можем вырезать одну из тех клеток, которая в первой раскраске имеют цвет 1, а во второй 2. Таких клеток только 4 (см. рисунок 5), которые закрашены красным цветом.
На рисунке-6 показан пример заполнения доски прямоугольниками 1×3 (или 3×1) с одной клеткой красного цвета. Примеры для остальных клеток можно получит поворотом доски.
б)(3m+2n)^2=(3m)^2-2*3*2mn+(2n)^2=9m^2+12mn+4n^2.
в)(7m-2)^2=(7*m)^2-2*2*7m+2^2=49m^2-28m+4
г)(8m-n)^2=(8m)^2-2*8m*n+n^2=64m^2-16mn+n^2