Поэтому K лежит на отрезке MH.
1.
Рассмотри ∠ACH и ∠ABC:
CA⊥BA и CH⊥BH по условию;
∠ACH = ∠ABC, как углы с взаимно перпендикулярными сторонами.
Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.Поэтому CM = BM, тогда ΔBMC - равнобедренный.
Углы при основании равнобедренного треугольника равны.Поэтому ∠MBC = ∠MCB, откуда ∠ACH = ∠MCB (т.к. ∠ACH = ∠MBC).
∠ACK = ∠BCK, как углы при биссектрисе;
∠ACH = ∠MCB;
Тогда ∠ACK - ∠ACH = ∠BCK - ∠MCB;
∠HCK = ∠MCK.
Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.2.
Рассмотрим ΔMCH:
CK - биссектриса MCH, поскольку ∠HCK = ∠MCK;
Тогда справедливо равенство  ;
;
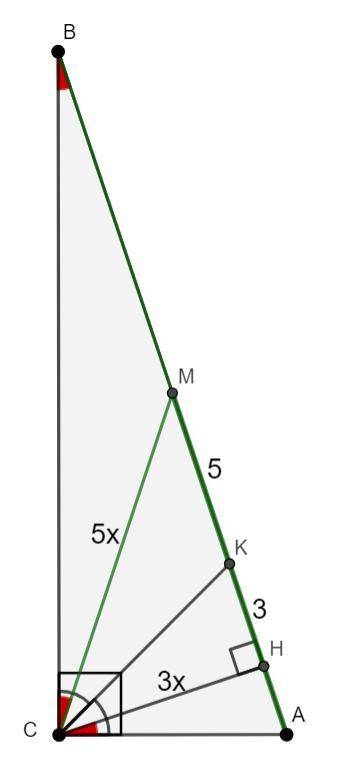
Пусть CM = 5x, тогда CH = 3x;
HM = HK+KM = 3+5 = 8;
ΔMCH - прямоугольный (CH⊥MH ⇒ ∠CHM = 90°);
Тогда по теореме Пифагора получим:
CH²+HM² = CM²;
(3x)²+8² = (5x)²;
9x²+64 = 25x²;
64 = 16x²;
x² = 64:16 = 2²;
x = 2.
CM = 5x = 5·2 = 10;
CH = 3x = 3·2 = 6.
3.
CM = BM = MA;
MA = 10;
AB = 2·MA = 2·10 = 20;
AH = MA-HM = 10-8 = 2.
4.
Рассмотрим ΔCHA:
∠CHA = 90°; AH = 2; CH = 6;
По теореме Пифагора найдём AC:
AC² = CH²+AH² = 6²+2² = 36+4 = 2²·10;
AC = 2√10.
5.
Рассмотрим ΔABC:
∠ACB = 90°; AC = 10√2; AB = 20;
По теореме Пифагора надём BC:
BC² = AB²-AC² = 20²-40 = 400-40 = 6²·10;
BC = 6√10.
6.
Рассмотрим ΔCHK:
∠CHK = 90°; CH = 6; HK = 3;
По теореме Пифагора найдём CK:
CK² = CH²+HK² = 6²+3² = 36+9 = 3²·5;
CK = 3√5.
ответ: AB = 20; BC = 6√10; AC = 2√10; CK = 3√5.
Вычислим сумму:
52 + 287 + 48 + 13 =
В этом выражении есть числа, при сложении которых получаются «круглые» числа. Заметив это, легко провести вычисления устно. Воспользуемся переместительным законом сложения.

Также для упрощения вычисления произведений можно использовать переместительный закон умножения.
7 · 2 · 9 · 5 = (2 · 5) · (7 · 9) = 10 · 63 = 630
Сочетательные и переместительные свойства используются и при упрощении буквенных выражений.
6 · a · 2 = 6 · 2 · a = 12a2 · a · 4 · b = 2 · 4 · a · b = 8ab5b + 8b = (5 + 8) · b = 13b14y − 12y = (14 − 12) · y = 2y
Распределительный закон умножения часто применяется для упрощения вычислений.

Применяя распределительное свойство умножения относительно сложения или вычитания к выражению (a + b) · с и (a − b) · c, мы получаем выражение, не содержащее скобки.
В этом случае говорят, что мы раскрыли (опустили) скобки. Для применения свойств не имеет значения, где записан множитель «c» — перед скобками или после.
Раскроем скобки в выражениях.
2(t + 8) = 2t + 16(3x − 5)4 = 4 · 3x − 4 · 5 = 12x − 20
Запомните!
Если перед буквой не записано число, то подразумевается, что перед буквой стоит числовой множитель 1.
t + 4t = (1 + 4)t = 5t
Вынесение общего множителя за скобки
Поменяем местами правую и левую часть равенства:
(a + b)с = ac + bc
Получим:
ac + bc = (a + b)с
В таких случаях говорят, что из «ac + bc»вынесен общий множитель «с» за скобки.
Примеры вынесения общего множителя за скобки.
73 · 8 + 7 · 8 = (73 + 7) · 8 = 80 · 8 = 6407x − x − 6 = (7 − 1)x − 6 = 6x − 6 = 6(x − 1)