Пошаговое объяснение:
(x-5)(x+3) >0
сначала находим точки нуля (x-5)(x+3)=0 ⇒ х₁ = 5; х₂= -3
теперь наносим точки на прямую и смотрим знаки функции
(берем любую точку интервала и считаем функцию)
(-∞; -3) f(-4) = 9 > 0 этот интервал подходит
(-3;5) f(0)=15 < 0 этот интервал не подходит
(5;+∞) f(6) = 9 > 0 этот интервал подходит
ответ x ∈ (− ∞ ;−3)∪(5;+ ∞) или х < -3; x > 5
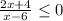
всё по тому же сценарию
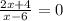домножим правую и левую часть на (х-6),
получим 2х+4 = 0; х₁ = -2
и еще имеем точку х₂=6, поскольку домножили на (х-6)
(-∞; -2) f(-3) = -2/(-9) = 2/9 > 0 этот интервал не подходит
[-2; 6) f(0)= 4/(-6) < 0 этот интервал подходит
(6; +∞) f(7) = 18/1 > 0 этот интервал не подходит
значит ответ х ∈ [-2; 6)
1.
1) Выразим у через х.
-2x + y = 8
y = 8 + 2x
Теперь, подставим у, выраженное через х в первое уравнение:
-2х + (8 + 2х) = 8
Раскроем скобки:
-2х + 2х + 8 = 8
Мы видим, что иксы взаимоуничтожаются, так что уравнение равно при любом х.
Например, при х = 1:
у = 8 + 2*1 = 10, подставляем в исходное уравнение: -2*1 + 10 = 8 - верное равенство.
Возьмём х = 2 : у = 8 + 2*2 = 12 => -2*2 + 12 = 8
2)Решаем также:
х - 3у=6
-3у = 6 - х
3у = х - 6
у = (х - 6) / 3
Решения находим также:
х = 3 => у = (3-6) / 3 = -1
3 -3 * (-1) = 3 + 3 = 6 - всё верно.
х=10 => у = (10 - 6 ) / 3 = 4/3
10 - 3 * 4/3 = 10 - 4 = 6 - всё верно.
2.
1) 4х - у = 8
4х = 8 + у
х = (8 + у) / 4
у = 4 => x = (8 + 4) / 4 = 3
исх. уравнение: 4*3 - 4 = 12 - 4 =8
y = 0 = > x = (8 + 0) / 4 = 2
исх. уравнение: 4*2 - 0 = 8
2) х + 3у = -2
х = -2 - 3у
у = 3 => x = -2 - 3*3 = -11
исх. уравнение: -11 + 3*3 = -2
у = 5 => х = -2 -3*5 = -17
исх. уравнение: -17 + 15 = -2
3. 3х + у = 6
Приводим к стандартному виду:
у = 6 -3х
( таблица)
x | 0 | 1 |
y | 6 | 3 |
