Оценка:
Пусть операции изменения цвета клетки происходят поочерёдно (если в какой-то момент нужно изменить сразу несколько клеток, изменим их по очереди). Так как каждая новая чёрная клетка касается хотя бы двух предыдущих, то при операции изменения цвета клетки общий периметр чёрных клеток не увеличивается. В конце он должен будет стать равным 44, следовательно, он был не меньше 44 изначально (не менее 11 клеток).
Пример:
Довольно очевидным будет то, что если изначально все чёрные клетки располагались на главной диагонали, то таблица станет полностью чёрной.
ответ: 11 клеток.
Поскольку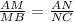 
, то треугольники MAN и BAC подобны. Значит MN параллелен BC ⇔ BMNC - трапеция. При этом BN и MC - диагонали. В трапеции отрезок, соединяющий середины оснований, продолжения боковых сторон и точка пересечения диагоналей лежат на одной прямой. Следовательно, AT - медиана треугольника ABC. Заметим, что отношение "расстояний" пройденных точками A и O равно искомому отношению диаметров окружностей, что равно отношению радиусов. Точка T зафиксирована. Спроецируем путь пройденный точкой O на вертикальную ось. Получим длину диаметра окружности. Данный диаметр пропорционален длине отрезка OT. Точка A пройдет весь путь окружности, проекция этого пути равна диаметру описанной окружности. Так как точка O лежит на отрезке AT, то пройденный путь пропорционален диаметру описанной окружности с тем же коэффициентом пропорциональности, что и отношение отрезка OT к соответствующему пути. Получили, что искомое отношение радиусов равно отношению 
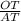. Пусть MB = x, AM = 3x; AN = 3y; NC = y; TC = BT; По теореме Менелая: 
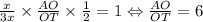, Значит 
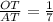; ответ: 7:1
